Задан функциональный граф — такой ориентированный граф, в котором из каждой вершины выходит ровно одна дуга. Вершины графа пронумерованы от 0 до n - 1.
Граф задан массивом f0, f1, ..., fn - 1, где fi — номер вершины, куда ведет единственная дуга из вершины i. Кроме того задан массив весов дуг w0, w1, ..., wn - 1, где wi — вес дуги из i в fi.
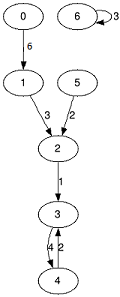Граф из первого примера. По заданному числу k (длине пути) найдите для каждой вершины пару чисел: si и mi, где:
- si — сумма весов всех дуг на пути длины k, который стартует из вершины i;
- mi — минимальный вес по всем дугам на пути длины k, который стартует из вершины i.
Длиной пути называется количество дуг в этом пути.
Выходные данные
Выведите n строк, по два числа si, mi в каждой строке.
Примеры
| № | Входные данные | Выходные данные |
|
1
|
7 3
1 2 3 4 3 2 6
6 3 1 4 2 2 3
|
10 1
8 1
7 1
10 2
8 2
7 1
9 3
|
|
2
|
4 4
0 1 2 3
0 1 2 3
|
0 0
4 1
8 2
12 3
|
|
3
|
5 3
1 2 3 4 0
4 1 2 14 3
|
7 1
17 1
19 2
21 3
8 1
|