Маленький золотой медвежонок Нивел долго жил в лесу. Созерцать деревья ежедневно ему в какой-то момент порядком надоело, и он переехал в большой город.
В городе Нивел устроился управляющим медвежьей доставки. Город, в котором он поселился, можно представить как ориентированный граф из n вершин и m рёбер. У каждого ребра есть пропускная способность, равная максимальному количеству веса, который можно пронести по этому ребру в рамках одного цикла доставки. Доставка заключается в том, что каждый имеющийся у Нивела медвежонок несёт в своих лапках груз из вершины 1 в вершину n. Суммарный вес, пронесённый всеми медвежатами по ребру, не должен превышать пропускной способности этого ребра.
В подчинении у Нивела ровно x медвежат. Чтобы всё было честно, никто из медвежат не должен отдыхать и каждый медвежонок должен доставить из 1 в n груз одинакового веса. Однако медвежата вполне могут пойти разными дорогами.
Нивел хочет определить, какой максимальный суммарный вес может быть доставлен из вершины 1 в вершину n.
Выходные данные
Выведите единственное вещественное число — максимальный суммарный вес, который можно доставить из вершины 1 в вершину n, используя ровно x медвежат, каждый из которых пронесёт одинаковый вес. Ваш ответ будет считаться правильным, если его абсолютная или относительная ошибка не будет превосходить 10 - 6.
А именно: пусть ваш ответ равен a, а ответ жюри — b. Проверяющая программа будет считать ваш ответ правильным, если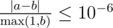 
.
Примечание
Доступны три медвежонка. Двое из них могут пойти по пути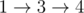 
, а третий по пути 
. Хотя медвежонок, идущий по пути , мог бы нести одну единицу веса, из-за зашкаливающей честности он не может взять с собой больше 0.5 единиц веса. Таким образом, суммарно будет доставлено 1.5 единиц веса. Обратите внимание, что, используя всего двух медвежат, можно было бы доставить 2 единицы веса, но Нивел обязан использовать всех трёх.
Примеры
| № | Входные данные | Выходные данные |
|
1
|
4 4 3
1 2 2
2 4 1
1 3 1
3 4 2
|
1.5000000000
|
|
2
|
5 11 23
1 2 3
2 3 4
3 4 5
4 5 6
1 3 4
2 4 5
3 5 6
1 4 2
2 5 3
1 5 2
3 2 30
|
10.2222222222
|