Как подобает любому порядочному школьнику, Кевин Сан изучает коровометрию, коровоматику и криптобычество в Буреновском государственном университете (БГУ) под руководством Фермера Ивана. На последнем занятии по математическому упрощению уравнений (МУУ) Кевин столкнулся со странным функциональным уравнением, для решения которого он нуждается в вашей помощи. Даны два целых числа k и p, при этом p — нечётное простое число и функциональное уравнение:
для некоторой функции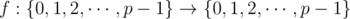 
. (Равенство должно выполняться для любого целого x от 0 до p - 1 включительно).
Кевин просит вас посчитать количество различных функций f, удовлетворяющих этому уравнению. Поскольку ответ может быть достаточно большим, вы должны вывести остаток от деления этого числа на 109 + 7.
Выходные данные
Выведите единственное целое число — количество различных функций f, удовлетворяющих уравнению, по модулю 109 + 7.
Примечание
В первом примере p = 3 и k = 2. Подходят следующие функции:
- f(0) = 0, f(1) = 1, f(2) = 2.
- f(0) = 0, f(1) = 2, f(2) = 1.
- f(0) = f(1) = f(2) = 0.
Примеры
| № | Входные данные | Выходные данные |
|
1
|
3 2
|
3
|
|
2
|
5 4
|
25
|