На плоскости расположены n точек (xi, yi) с целочисленными координатами от 0 до 106. Расстоянием между двумя точках с номерами a и b назовем следующую величину: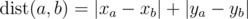 
(расстояние, вычисляемое по такой формуле, называется манхеттенским расстоянием).
Назовем гамильтоновым путем некоторую перестановку pi от 1 до n. Назовем длиной этого пути величину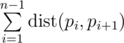 
.
Найдите какой-нибудь гамильтонов путь с длиной не более, чем 25 × 108. Обратите внимание, минимизировать длину гамильтонова пути не требуется.
Выходные данные
Выведите перестановку чисел pi от 1 до n — искомый гамильтонов путь. Перестановка должна удовлетворять неравенству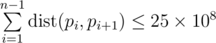 
.
Если возможных ответов несколько, разрешается вывести любой.
Гарантируется, что существует подходящая перестановка.
Примечание
В тесте из условия, суммарное расстояние равно:
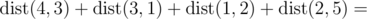
(|5 - 3| + |0 - 4|) + (|3 - 0| + |4 - 7|) + (|0 - 8| + |7 - 10|) + (|8 - 9| + |10 - 12|) = 2 + 4 + 3 + 3 + 8 + 3 + 1 + 2 = 26
Примеры
| № | Входные данные | Выходные данные |
|
1
|
5
0 7
8 10
3 4
5 0
9 12
|
4 3 1 2 5
|