Лиса Ciel участвует в вечеринке в Простом королевстве. На вечеринку приглашены n лис (включая саму Ciel). i-й из приглашённых лис ai лет.
Ужин будет проходить за несколькими круглыми столами. Требуется распределить лис по столам так, что:
- Каждая лиса окажется за некоторым столом.
- За каждым столом сидит не менее 3 лис.
- Сумма возрастов любых двух соседних лис за каждым столом должна быть простым числом.
Если k лис f1, f2, ..., fk сидят за столом по часовой стрелке, то для 1 ≤ i ≤ k - 1 fi и fi + 1 соседние, а также f1 и fk тоже являются соседними.
Если можно распределить лис требуемым образом, найдите способ сделать это.
Выходные данные
Если распределить лис указанным образом невозможно, выведите «Impossible» (без кавычек).
В противном случае, в первой строке выведите целое число m (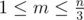
) — количество столов.
Затем выведите m строк. Каждая строка должна начинаться с целого числа k, количества лис за столом, затем должны следовать k чисел — индексы лис, сидящих за этим столом, по часовой стрелке.
Если возможных распределений несколько, выведите любое.
Примечание
В первом примере можно усадить всех лис за один стол указанным образом. Их возрасты: 3 – 8 – 9 – 4, суммы возрастов соседних лис: 11, 17, 13 и 7, все эти числа являются простыми.
Во втором примере это невозможно: сумма 2 + 2 = 4 не является простым числом.
Примеры
| № | Входные данные | Выходные данные |
|
1
|
4
3 4 8 9
|
1
4 1 2 4 3
|
|
2
|
5
2 2 2 2 2
|
Impossible
|
|
3
|
12
2 3 4 5 6 7 8 9 10 11 12 13
|
1
12 1 2 3 6 5 12 9 8 7 10 11 4
|
|
4
|
24
2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
|
3
6 1 2 3 6 5 4
10 7 8 9 12 15 14 13 16 11 10
8 17 18 23 22 19 20 21 24
|