Маленький Витя очень любит теорию множеств (напомним, что множество — это набор чисел, в котором все числа попарно различны). Сегодня Витя хочет найти множество целых чисел S, обладающее следующими свойствами:
- для всех x
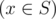выполняется неравенство l ≤ x ≤ r; - 1 ≤ |S| ≤ k;
- обозначим i-й по порядку элемент множества S как si; значение
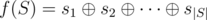как можно меньше.
Помогите Вите найти описанное множество.
Выходные данные
Выведите минимально возможное значение f(S). Затем выведите мощность множества |S|. Затем сами элементы множества в любом порядке.
Если существует несколько оптимальных множеств, разрешается вывести любое.
Примечание
Операция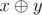 
обозначает операцию побитого исключающего ИЛИ. Другими словами, операцию XOR.
Примеры
| № | Входные данные | Выходные данные |
|
1
|
8 15 3
|
1
2
10 11
|
|
2
|
8 30 7
|
0
5
14 9 28 11 16
|