На этот раз наш ребенок раздобыл простой многоугольник. Ему надо найти количество способов разбить многоугольник на невырожденные треугольники таким образом, что:
- каждая вершина каждого треугольника — это одна из вершин многоугольника;
- каждая сторона многоугольника должна быть стороной ровно одного треугольника;
- площадь пересечения любых двух треугольников равна нулю, а сумма всех площадей треугольников равна площади многоугольника;
- каждый треугольник полностью расположен внутри многоугольника;
- каждая сторона каждого треугольника должна содержать ровно две вершины многоугольника.
Ниже приведен рисунок, показывающий пример корректного разбиения.
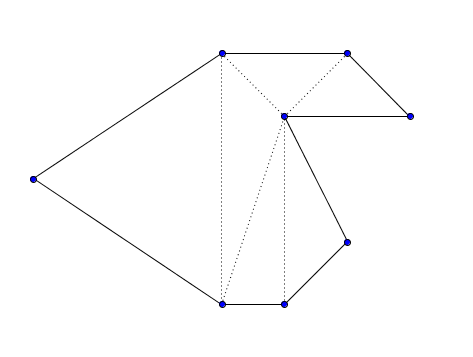
Пожалуйста, помогите ребенку. Посчитайте описанное количество способов по модулю 1000000007 (109 + 7) для него.
Выходные данные
Выведите количество способов по модулю 1000000007 (109 + 7).
Примечание
В первом примере существует два возможных разделения:
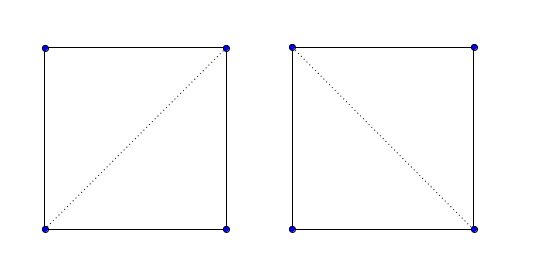
Во втором примере есть только одно возможное разделение:
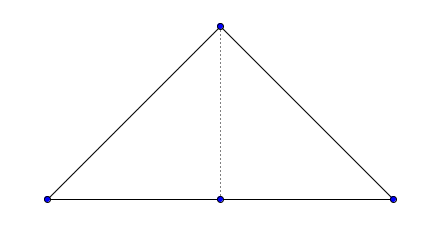
Примеры
| № | Входные данные | Выходные данные |
|
1
|
4
0 0
0 1
1 1
1 0
|
2
|
|
2
|
4
0 0
1 0
0 1
-1 0
|
1
|
|
3
|
5
0 0
1 0
1 1
0 1
-2 -1
|
3
|