К нам едет министр образования! Разумеется, никто не хочет ударить в грязь лицом перед таким высокопоставленным гостем. Но буквально за два часа до визита выяснилось, что в одном из классов не работает лампочка — ей, видите ли, энергии недостаточно. Решение проблемы нашлось быстро: нужно всего лишь выбрать местоположение лампочки так, чтобы она получала максимальное количество энергии.
Все знают, что мощность лампочки равна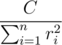 
, где C — некоторая константа, а ri — евклидово расстояние от лампочки до i-го генератора. Следовательно, нам нужно минимизировать 
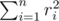. Конечно, местоположение всех генераторов мы знаем.
Лампочка должна находиться на потолке класса. Потолок класса имеет форму строго-выпуклого m-угольника (сам класс имеет вид прямой призмы со строго-выпуклым m-угольником в основании). Помогите найти оптимальное местоположение лампочки. Считайте, что все генераторы находятся в плоскости потолка класса. Считайте, что в плоскости потолка класса введена некоторая декартова система координат.
Выходные данные
Выведите единственное вещественное число — минимальное значение суммы квадратов расстояний до генераторов от точки оптимального расположения лампочки. Ответ будет считаться правильным, если его относительная или абсолютная погрешность не будет превышать 10 - 4.
Примечание
Многоугольник называется строго-выпуклым, если он выпуклый, и никакие три его вершины не лежат на одной прямой.
Примеры
| № | Входные данные | Выходные данные |
|
1
|
4
3 2
3 4
5 4
5 2
4
3 3
4 4
5 3
4 2
|
8.00000000
|