На олимпиаде по информатике программисту Ксюше попалась задача на строки. К сожалению, Ксюша не сильна в строковых алгоритмах. Помогите ей решить задачу.
Строкой s назовем последовательность символов s1s2... s|s|, где записью |s| будем обозначать длину строки.
Подстрокой s[i... j] строки s будем называть строку sisi + 1... sj.
Строка s является строкой Грея, если она удовлетворяет условиям:
- длина строки |s| нечетная;
- символ
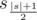встречается в строке ровно один раз; - либо |s| = 1, либо подстрок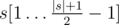и
и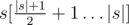 
равны между собой и являются строками Грея.
Например, строки «abacaba», «xzx», «g» являются строками Грея, а строки «aaa», «xz», «abaxcbc» — нет.
Красотой строки p называется сумма квадратов длин всех подстрок строки p, которые являются строками Грея. Другими словами, рассмотрим все пары значений i, j (1 ≤ i ≤ j ≤ |p|). Если подстрока p[i... j] является строкой Грея, к красоте нужно прибавить (j - i + 1)2.
В задаче Ксюше задана строка t, состоящая из символов латинского алфавита. Ей разрешается изменить не более одного символа этой строки на любой другой символ латинского алфавита. Задача состоит в том, чтобы получить строку как можно большей красоты.
Выходные данные
Выведите искомое максимальное значение красоты, которое удастся получить Ксюше.
Пожалуйста, не используйте спецификатор %lld для чтения или записи 64-битных чисел на С++. Рекомендуется использовать потоки cin, cout или спецификатор %I64d.
Примечание
В первом тестовом примере из заданной строки можно получить строку p = «zbz». В такой строке строками Грея являются подстроки p[1... 1], p[2... 2], p[3... 3] и p[1... 3]. Итого, красота строки p получается равна 12 + 12 + 12 + 32 = 12. Более красивую строку получить нельзя.
Во втором тестовом примере можно не применять никаких операций. Изначальная строка имеет наибольшую возможную красоту.