В один прекрасный день медведь Василий нарисовал на координатной плоскости 2m окружностей одинакового радиуса R. Окружности с номерами от 1 до m имели в качестве своих центров точки (2R - R, 0), (4R - R, 0), ..., (2Rm - R, 0) соответственно. Окружности с номерами от m + 1 до 2m имели в качестве своих центров точки (2R - R, 2R), (4R - R, 2R), ..., (2Rm - R, 2R) соответственно.
Конечно, медведь нарисовал окружности для того, чтобы провести простой эксперимент с мухой. Эксперимент затянулся на m2 дней. Каждый день эксперимента получил свой уникальный номер от 0 до m2 - 1 включительно.
В день с номером i происходило следующее:
- Муха прилетала на координатную плоскость в центр окружности с номером
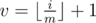 (
(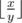 — результат деления числа x на число y, округленный вниз до целого числа).
— результат деления числа x на число y, округленный вниз до целого числа). - Муха шла по координатной плоскости в центр окружности с номером
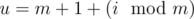 (
(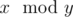 — остаток от деления числа x на число y). Медведь заметил, что муха шла из центра окружности v в центр окружности u по кратчайшему пути, все точки которого лежали на границе или внутри хотя бы одной из 2m окружностей. После того как муха приходила в центр окружности с номером u, она улетала в неизвестном направлении.
— остаток от деления числа x на число y). Медведь заметил, что муха шла из центра окружности v в центр окружности u по кратчайшему пути, все точки которого лежали на границе или внутри хотя бы одной из 2m окружностей. После того как муха приходила в центр окружности с номером u, она улетала в неизвестном направлении.
Помогите Василию, посчитайте среднее арифметическое расстояний, пройденных мухой по координатной плоскости за каждый из этих m2 дней.