Умный Бобер хочет быть не только умным, но и здоровым бобром! И поэтому он начал посещать уроки физкультуры в школе X. В этой школе занятия физкультурой ведет очень креативный преподаватель. Одним из его любимых разминочных упражнений является перебрасывание мячей. Ученики становятся в ряд. Каждый изначально получает один мяч. Мячи пронумерованы от 1 до n (требование комиссии по инвентаризации).
 Рисунок 1. Начальное положения для n = 5.
Рисунок 1. Начальное положения для n = 5. После получения мячей ученики выполняют разминочное упражнение. Упражнение проходит в несколько бросков. Для каждого из бросков учитель выбирает двух произвольных разных учеников, которые будут в нем участвовать. Выбранные ученики бросают друг другу свои мячи. Таким образом, после каждого броска ученики остаются на своих местах, а два мяча меняются местами.
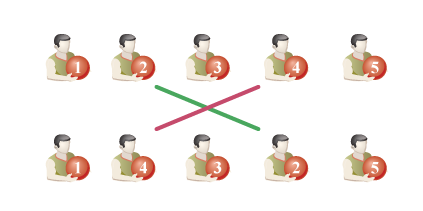 Рисунок 2. Пример броска.
Рисунок 2. Пример броска. В данном случае произошел бросок между учениками, которые держали 2-й и 4-й мячи. Так как упражнений в разминке немало, то на каждое из них выделяется немного времени. Поэтому для каждого ученика известно, в каком максимальном числе бросков он может принять участие. В рамках рассматриваемых уроков физкультуры, это число 1 или 2.
Заметим, что после всех этапов рассматриваемого упражнения любой из мячей может оказаться у любого из учеников. Умный Бобер решил формализовать это и ввел понятие «порядок мячей». Порядок мячей — это последовательность из n чисел, которая соответствует порядку мячей в строю. Первое число будет соответствовать номеру мяча у первого слева ученика в строю, второе — номеру мяча у второго ученика и так далее. Например, на рисунке 2 порядок мячей был (1, 2, 3, 4, 5), а после броска стал (1, 4, 3, 2, 5). Умный бобер знает количество учеников и для каждого из учеников максимальное число бросков, в которых данный ученик может принять участие. И теперь ему стало любопытно, каково количество различных вариантов порядка мячей после окончания упражнения.