Байк увлекается перестановками. Перестановка длины n представляет собой последовательность целых чисел, такую, что каждое число от 0 до (n - 1) встречается в ней ровно один раз. Например, [0, 2, 1] — это перестановка длины 3, а вот [0, 2, 2] и [1, 2, 3] — нет.
Тройка перестановок длины n (a, b, c) называется Счастливой Тройкой Перестановок тогда и только тогда, когда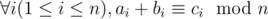 
. Переменная ai обозначает i-ый элемент перестановки a. Описанное выше модульное равенство означает, что остатки после деления ai + bi на n и деления ci на n равны.
Теперь у Байка есть целое число n и он хочет найти Счастливую Тройку Перестановок. Пожалуйста, помогите ему!
Выходные данные
Если не существует Счастливой Тройки Перестановок длины n, выведите -1.
В противном случае следует вывести три строки. В каждой строке содержится по n целых чисел через пробел. В первой строке надо вывести перестановку a, во второй — перестановку b, в третьей — перестановку c.
Если ответов несколько, выведите любой.
Примечание
В примере 1, тройка перестановок ([1, 4, 3, 2, 0], [1, 0, 2, 4, 3], [2, 4, 0, 1, 3]) является счастливой, так как выполняются следующие условия:
В примере 2 легко заметить, что счастливых троек перестановок вообще нет.
Примеры
| № | Входные данные | Выходные данные |
|
1
|
5
|
1 4 3 2 0
1 0 2 4 3
2 4 0 1 3
|
|
2
|
2
|
-1
|