Вам задана неубывающая последовательность x1, x2, ..., xn (1 ≤ x1 ≤ x2 ≤ ... ≤ xn ≤ q). Также Вам заданы два целых числа a и b (a ≤ b; a·(n - 1) < q).
Ваша задача преобразовать последовательность x1, x2, ..., xn в некоторую последовательность y1, y2, ..., yn (1 ≤ yi ≤ q; a ≤ yi + 1 - yi ≤ b). Определим стоимость преобразования как сумму: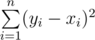 
. Требуется выбрать такую последовательность y, что описанная стоимость преобразования минимальна.
Выходные данные
В первой строке выведите n вещественных чисел — искомую последовательность y1, y2, ..., yn (1 ≤ yi ≤ q; a ≤ yi + 1 - yi ≤ b). Во второй строке выведите минимальную стоимость преобразования, то есть .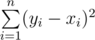
Если существует несколько оптимальных ответов, можно вывести любой из них.
Ответ будет считаться правильным, если относительная или абсолютная погрешность не будет превышать 10 - 6.
Примеры
| № | Входные данные | Выходные данные |
|
1
|
3 6 2 2
1 4 6
|
1.666667 3.666667 5.666667
0.666667
|
|
2
|
10 100000 8714 9344
3378 14705 17588 22672 32405 34309 37446 51327 81228 94982
|
1.000000 8715.000000 17429.000000 26143.000000 34857.000000 43571.000000 52285.000000 61629.000000 70973.000000 80317.000000
797708674.000000
|