Дима и Аня любят играть в разные игры. Сейчас Дима придумал новую игру, в которую хочет поиграть с Аней.
Дима пишет на листке n пар целых чисел (li, ri) (1 ≤ li < ri ≤ p). Далее игроки ходят по очереди. За один ход игрок может выполнить следующее действие:
- выбрать номер пары i (1 ≤ i ≤ n), такой что ri - li > 2;
- заменить пару номер i на пару
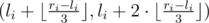или на пару 
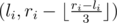. Запись ⌊x⌋ обозначает округление к ближайшему меньшему целому числу.
Игрок, который не может сделать ход — проигрывает.
Конечно, Дима хочет, чтобы Аня, которая будет ходить первая, выиграла. Поэтому Дима должен выписать такие n пар целых чисел (li, ri) (1 ≤ li < ri ≤ p), чтобы при оптимальной игре обоих игроков выигрывал первый. Посчитайте, сколькими способами Дима может это сделать. Выведите остаток от деления ответа на число 1000000007 (109 + 7).
Два способа считаются различными, если различаются упорядоченные последовательности выписанных пар.