Вы раскрашиваете бесконечную клетчатую плоскость, на которой все клетки изначально белые. Для этого вам дается \(n\) штампов. Каждый штамп является прямоугольником ширины \(w_i\) и высоты \(h_i\).
Вы примените каждый штамп ровно один раз, чтобы окрасить в чёрный цвет прямоугольник того же размера, что и штамп. Вы не можете поворачивать штамп; каждая клетка должна быть либо полностью покрыта штампом, либо не покрыта. Вы можете использовать штамп на любом прямоугольнике из клеток плоскости, даже если некоторые или все клетки, покрытые областью штампа, уже черные.
Какую минимальную сумму периметров связных областей черных квадратов можно получить после использования всех штампов?
Выходные данные
Для каждого набора входных данных выведите одно целое число — минимальную сумму периметров связных областей черных квадратов, которую можно получить после использования всех штампов.
Примечание
В первом наборе входных данных можно использовать штампы, как показано слева. Каждый штамп выделен своим цветом для наглядности.
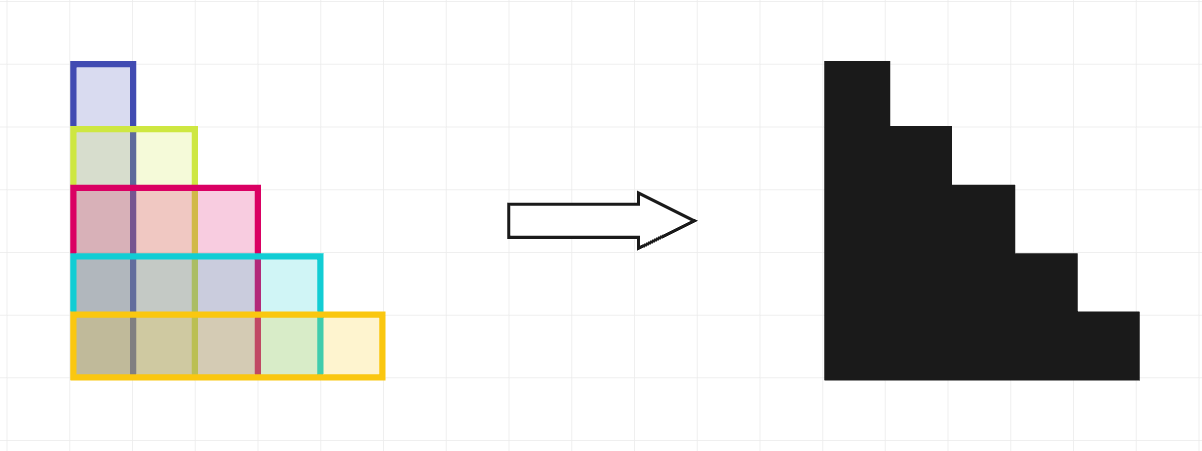
После использования всех штампов осталась одна черная область (как показано справа), периметр которой равен \(20\). Можно показать, что не существует способа использования штампов, который дал бы меньший общий периметр.
Во втором наборе входных данных второй и третий штампы могут быть использованы полностью внутри первого, поэтому ответ — \(8\).
Примеры
| № | Входные данные | Выходные данные |
|
1
|
5
5
1 5
2 4
3 3
4 2
5 1
3
2 2
1 1
1 2
1
3 2
3
100 100
100 100
100 100
4
1 4
2 3
1 5
3 2
|
20
8
10
400
16
|