Красивая двоичная матрица — это матрица, по краям которой стоят единицы, а внутри нули.
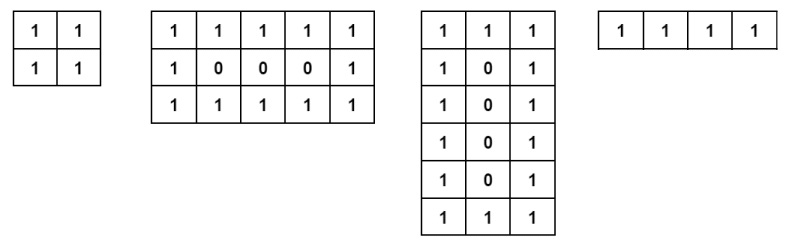Примеры четырёх красивых двоичных матриц. Сегодня Сакурако играла с красивой двоичной матрицей размера \(r \times c\) и сделала из неё двоичную строку \(s\), выписав все строки матрицы, начиная с первой и заканчивая \(r\)-й. Более формально, элемент из матрицы в \(i\)-й строке и \(j\)-м столбце совпадает с \(((i-1)*c+j)\)-м элементом строки.
Необходимо проверить, могла ли красивая матрица, из которой получена строка \(s\), быть квадратной. Иными словами, вам надо проверить, могла ли строка \(s\) быть получена из квадратной красивой бинарной матрицы (то есть такой, что \(r=c\)).
Выходные данные
Выведите «Yes», если исходная матрица могла быть квадратной, и «No» иначе.
Примечание
Во втором примере из матрицы можно получить строку 1111:
В третьем примере строка 111101111 может быть получена из матрицы:
| \(1\) | \(1\) | \(1\) |
| \(1\) | \(0\) | \(1\) |
| \(1\) | \(1\) | \(1\) |
В четвёртом примере не существует квадратной матрицы, из которой можно получить строку.
Примеры
| № | Входные данные | Выходные данные |
|
1
|
5
2
11
4
1111
9
111101111
9
111111111
12
111110011111
|
No
Yes
Yes
No
No
|