У вас есть массив \(a\) размера \(n\).
Отрезок \([l, r](1 \le l < r \le n)\) называется многоугольным отрезком в том случае, если выполняются следующие условия:
- \((r-l+1) \geq 3\);
- Используя \(a_l, a_{l+1}, \ldots, a_r\) в качестве длин сторон, эти стороны могут образовать многоугольник с \((r-l+1)\) стороной.
Обработайте \(q\) запросов двух типов:
- «1 l r»: найти длину самого длинного отрезка среди всех многоугольных отрезков \([l_0,r_0]\), удовлетворяющих условию \(l \le l_0 \le r_0 \le r\). Если такого многоугольного отрезка нет, выведите вместо этого \(-1\);
- «2 i x»: присвоить \(a_i := x\).
Выходные данные
Для каждого запроса, если подходящего отрезка нет, выведите в отдельной строке \(-1\). В противном случае выведите длину самого длинного отрезка, удовлетворяющего вышеприведенному условию.
Примечание
В первом запросе первого набора входных данных не существует многоугольного отрезка. Например, если взять отрезок \([1,3]\), нельзя сделать треугольник со сторонами \(a_1=3\), \(a_2=1\) и \(a_3=2\).
Во втором запросе первого набора входных данных самый длинный многоугольный отрезок — \([1,4]\). Вы можете сделать четырехугольник со сторонами \(a_1=3\), \(a_2=1\), \(a_3=2\) и \(a_4=2\).
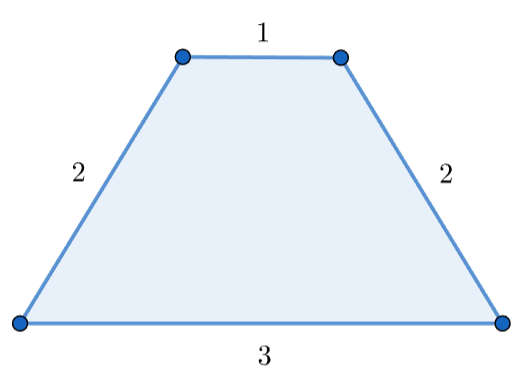Пример четырехугольника со сторонами \(3\), \(1\), \(2\) и \(2\).
Примеры
| № | Входные данные | Выходные данные |
|
1
|
2
5 6
3 1 2 2 8
1 1 3
1 1 4
1 1 5
2 1 5
1 1 4
1 1 5
4 10
500000000000 500000000000 1000000000000 500000000000
1 1 3
1 2 4
1 1 4
2 1 499999999999
2 3 999999999999
1 1 3
1 2 4
1 1 4
2 3 1000000000000
1 1 3
|
-1
4
4
3
5
-1
-1
4
-1
3
4
-1
|