Вам дана матрица \(n \times m\), где строки пронумерованы от \(1\) до \(n\) сверху вниз, а столбцы пронумерованы от \(1\) до \(m\) слева направо. Элемент на пересечении \(i\)-й строки и \(j\)-го столбца обозначим за \(a_{ij}\).
Рассмотрим алгоритм стабилизации матрицы \(a\):
- Найти клетку \((i, j)\), такую что ее значение строго больше значения всех соседних с ней клеток. Если такой клетки нет, завершить алгоритм. Если таких клеток несколько, то выбирается клетка с наименьшим значением \(i\), а если и таких несколько, то среди них с наименьшим значением \(j\).
- Сделать \(a_{ij} = a_{ij} - 1\).
- Перейти к шагу \(1\).
В этой задаче клетки \((a, b)\) и \((c, d)\) являются соседними, если у них есть общая сторона, то есть \(|a - c| + |b - d| = 1\).
Ваша задача вывести матрицу \(a\) после того, как будет запущен алгоритм стабилизации. Можно показать, что данный алгоритм не может выполняться бесконечное количество итераций.
Выходные данные
Для каждого набора входных данных выведите \(n\) строк по \(m\) чисел в каждой — значения клеток матрицы \(a\) после алгоритма стабилизации.
Примечание
В первом наборе входных данных два раза подряд алгоритм выберет клетку \((1, 1)\) и завершится.

Во втором наборе входных данных нет клетки, значение которой строго больше значений всех соседних клеток.
В третьем наборе входных данных алгоритм выберет клетку \((2, 2)\) и завершится.

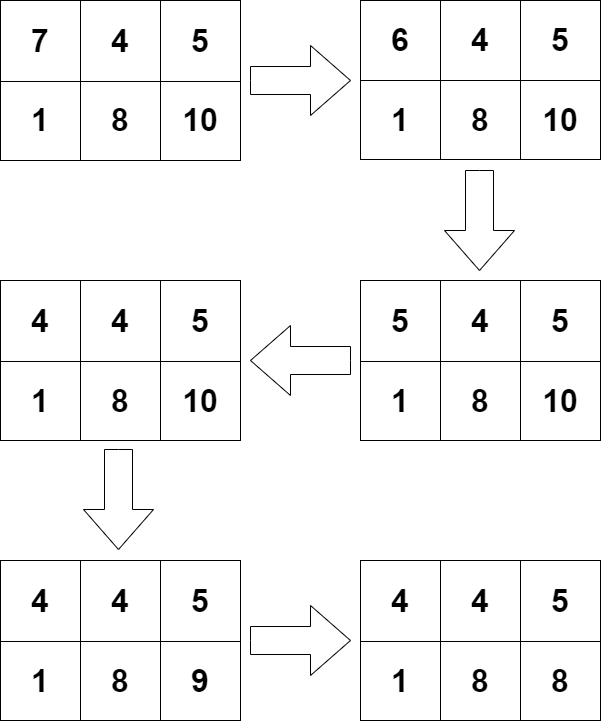
В четвертом наборе входных данных алгоритм три раза выберет клетку \((1, 1)\) и затем два раза клетку \((2, 3)\).
Примеры
| № | Входные данные | Выходные данные |
|
1
|
6
1 2
3 1
2 1
1
1
2 2
1 2
3 4
2 3
7 4 5
1 8 10
5 4
92 74 31 74
74 92 17 7
31 17 92 3
74 7 3 92
7 31 1 1
3 3
1000000000 1 1000000000
1 1000000000 1
1000000000 1 1000000000
|
1 1
1
1
1 2
3 3
4 4 5
1 8 8
74 74 31 31
74 74 17 7
31 17 17 3
31 7 3 3
7 7 1 1
1 1 1
1 1 1
1 1 1
|