В \(n\) различных точках \((x_1, y_1), (x_2, y_2), \ldots, (x_n, y_n)\) существует \(n\) башен, причем никакие три из них не являются коллинеарными, а четыре — конциклическими. Изначально вы владеете башнями \((x_1, y_1)\) и \((x_2, y_2)\), и хотите захватить их все. Для этого вы можете проделать следующую операцию любое количество раз:
- Выбрать две башни \(P\) и \(Q\), которыми вы владеете, и одну башню \(R\), которой вы не владеете, так, чтобы окружность, проходящая через точки \(P\), \(Q\) и \(R\) содержала все \(n\) башен внутри себя.
- После этого захватить все башни в или на треугольнике \(\triangle PQR\), включая сам \(R\).
План атаки — это последовательность выборов \(R\) (\(R_1, R_2, \ldots, R_k\)) в рамках вышеописанных операций, после которых вы захватываете все башни. Обратите внимание, что два плана атаки считаются различными, только если они отличаются выбором \(R\) в некоторой операции; в частности, два плана атаки с одинаковым выбором \(R\), но разными выборами \(P\) и \(Q\) считаются одинаковыми.
Подсчитайте количество планов атаки минимальной длины. Обратите внимание, что захватить все башни может быть невозможно, и в этом случае ответ будет равен \(0\).
Поскольку ответ может быть большим, выведите его по модулю \(998\,244\,353\).
Выходные данные
Для каждого набора входных данных выведите одно целое число — количество планов атаки минимальной длины, после которых вы захватите все башни, по модулю \(998\,244\,353\).
Примечание
В первом наборе входных данных существует только один возможный план атаки наименьшей длины, показанный ниже.
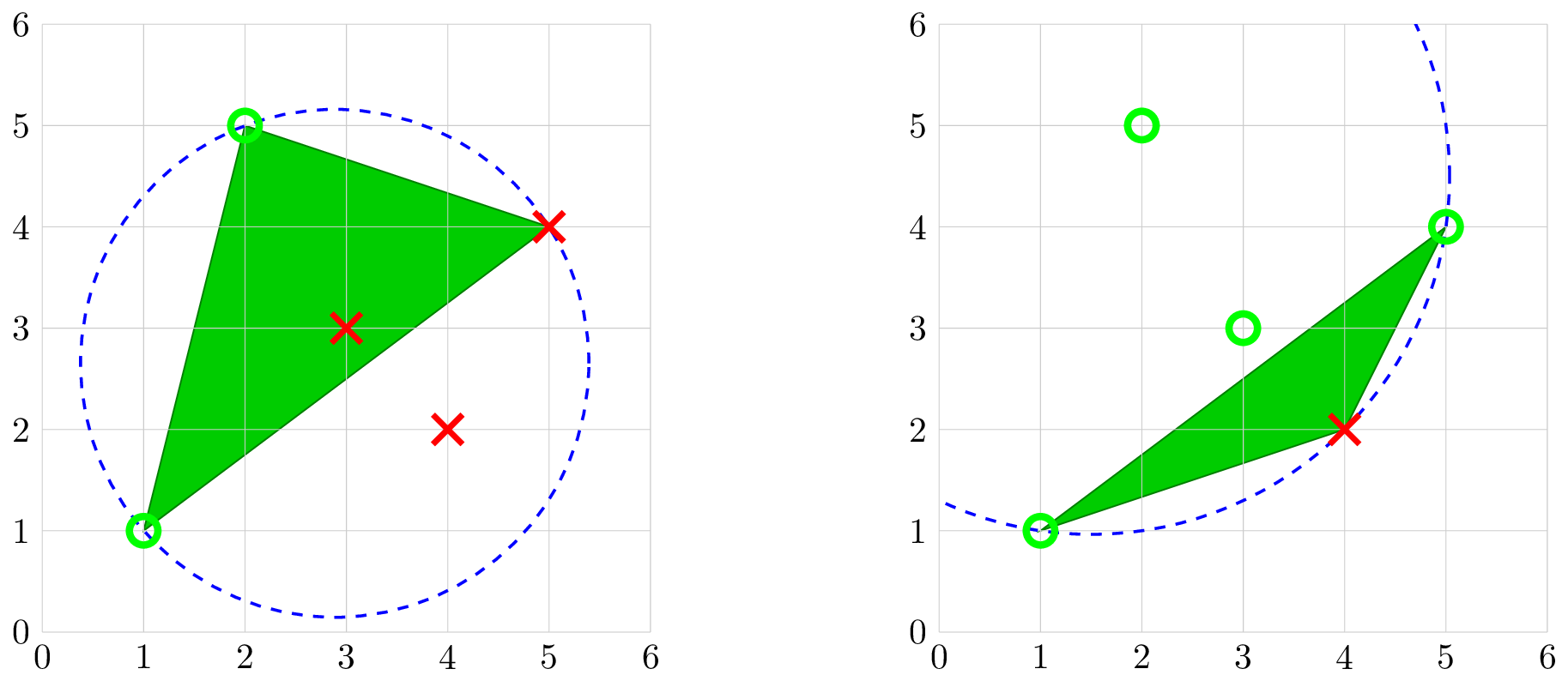
- Использовать операцию с башней \(P =\) \(1\), башней \(Q =\) \(2\) и башней \(R =\) \(5\). Окружность, проходящая через эти три башни, содержит все башни внутри себя, в результате чего башни \(3\) и \(5\) оказываются захваченными.
- Использовать операцию с башней \(P =\) \(5\), башней \(Q =\) \(1\) и башней \(R =\) \(4\). Окружность, проходящая через эти три башни, содержит все башни внутри себя, в результате чего башня \(4\) оказывается захваченной.
Во втором наборе входных данных, например, вы никогда не сможете захватить башню в точке \((3, 10\,000)\).
Примеры
| № | Входные данные | Выходные данные |
|
1
|
3
5
1 1
2 5
3 3
4 2
5 4
6
1 1
3 3
1 2
2 1
3 10000
19 84
7
2 7
-4 -3
-3 6
3 1
-5 2
1 -4
-1 7
|
1
0
10
|