Это усложнённая версия задачи, она отличается от упрощённой только поставленным вопросом.
Алиса и Боб делят поле. Поле представляет собой прямоугольник \(n \times m\) (\(2 \le n, m \le 10^9\)), строки пронумерованы от \(1\) до \(n\) сверху вниз, столбцы пронумерованы от \(1\) до \(m\) слева направо. Клетка на пересечении строки \(r\) и столбца \(c\) обозначается как (\(r, c\)).
У Боба есть \(k\) (\(2 \le k \le 2 \cdot 10^5\)) фонтанов, все из них расположены в разных клетках поля. Алиса отвечает за разделение поля, но должна соблюсти несколько условий:
- для разделения поля Алиса начнёт свой путь в любой свободной (без фонтана) клетке на левой или верхней стороне поля и будет перемещаться, каждый раз двигаясь на соседнюю клетку вниз или вправо, свой путь она закончит на правой или нижней стороне поля;
- этот путь Алисы разделит поле на две части — одна часть будет принадлежать Алисе (в эту часть включаются клетки её пути), другая — Бобу;
- Алисе будет принадлежать та часть, которая включает в себя клетку (\(n, 1\));
- Бобу будет принадлежать та часть, которая включает в себя клетку (\(1, m\)).
Алиса хочет разделить поле так, чтобы получить как можно больше клеток.
Боб хочет сохранить владение всеми фонтанами, но один любой из них подарить Алисе. Выведите сначала целое число \(\alpha\) — максимальный возможный размер участка Алисы, если Боб не подарит ей ни один фонтан (т.е. все фонтаны останутся на участке Боба).
Далее выведите \(k\) неотрицательных целых чисел \(a_1, a_2, \dots, a_k\), где \(a_i\) это такое значение, что после того как Боб подарит Алисе \(i\)-й фонтан максимальный размер её участка будет равен \(\alpha + a_i\).
Выходные данные
Для каждого набора входных данных сначала выведите \(\alpha\) — максимальный размер участка, который может принадлежать Алисе, если Боб не подарит ей ни один из фонтанов. В следующую строку выведите \(k\) неотрицательных целых чисел \(a_1, a_2, \dots, a_k\), где \(a_i\) это такое значение, что после того как Боб подарит Алисе \(i\)-й фонтан максимальный размер её участка будет равен \(\alpha + a_i\).
Примечание
Ниже приведены изображения для второго примера:
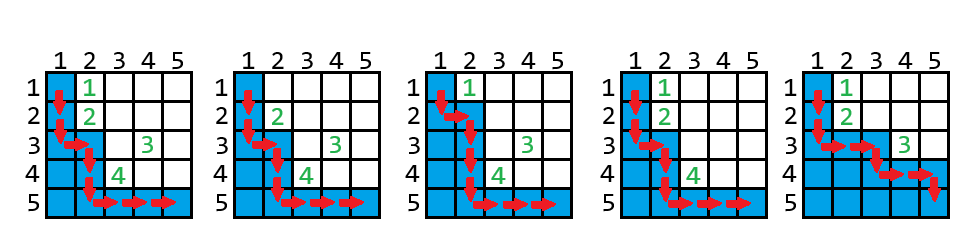Зелёным цветом подписаны номера фонтанов. Синим цветом обозначены клетки, принадлежащие Алисе. Обратите внимание, что если Боб дарит Алисе фонтан \(1\) или фонтан \(3\), то этот фонтан не может находиться на участке Алисы.
Примеры
| № | Входные данные | Выходные данные |
|
1
|
5
2 2 3
1 1
1 2
2 2
5 5 4
1 2
2 2
3 4
4 3
2 5 9
1 2
1 5
1 1
2 2
2 4
2 5
1 4
2 3
1 3
6 4 4
6 2
1 3
1 4
1 2
3 4 5
2 1
3 2
1 4
1 3
2 4
|
1
1 0 1
11
0 1 0 4
1
0 0 1 1 0 0 0 0 0
6
15 0 0 0
1
2 3 0 0 0
|