Манхэттенским расстоянием между двумя точками \((x_1, y_1)\) и \((x_2, y_2)\) называется величина, равная: \(\)|x_1 - x_2| + |y_1 - y_2|.\(\)
Назовем манхэттенским треугольником три точки на плоскости, манхэттенские расстояния между каждой парой из которых равны.
Вам дан набор попарно различных точек и четное целое число \(d\). Ваша задача — найти любой манхэттенский треугольник, составленный из трёх различных точек данного набора, у которого манхэттенское расстояние между любой парой вершин равно \(d\).
Выходные данные
Для каждого набора входных данных, выведите три целых попарно различных целых числа \(i\), \(j\) и \(k\) (\(1 \le i,j,k \le n\)) — индексы точек, образующих манхэттенский треугольник. Если ответа не существует, выведите «\(0\ 0\ 0\)» (без кавычек).
Если существует несколько решений, выведите любое из них.
Примечание
В первом наборе входных данных:
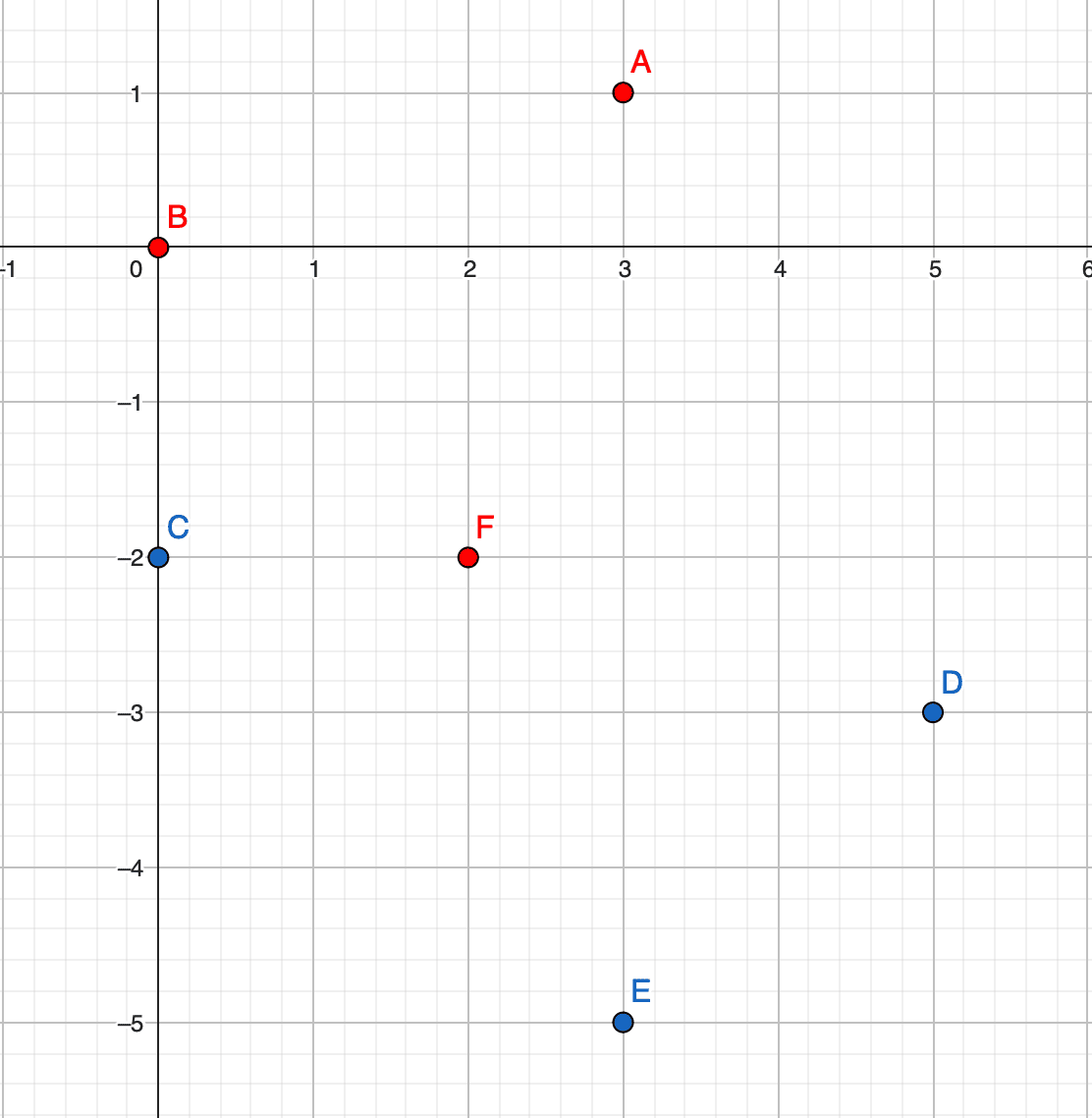Точки \(A\), \(B\) и \(F\) образуют манхэттенский треугольник, манхэттенское расстояние между каждой парой вершин равно \(4\). Точки \(D\), \(E\) и \(F\) также могут быть ответом. В третьем наборе входных данных:
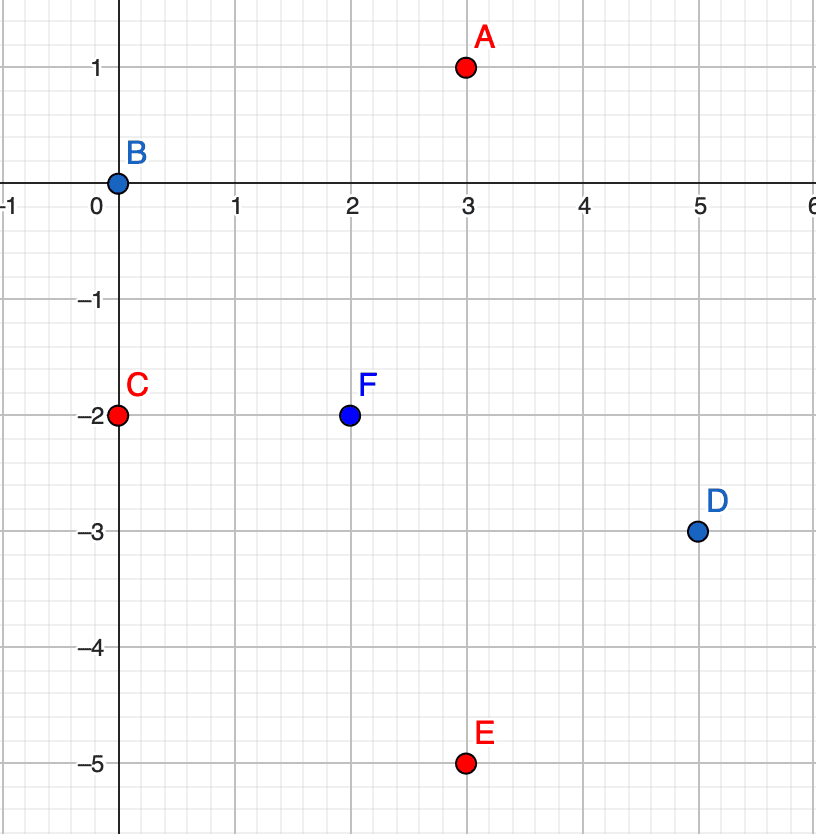Точки \(A\), \(C\) и \(E\) образуют манхэттенский треугольник, манхэттенское расстояние между каждой парой вершин равно \(6\). В четвертом наборе входных данных не существует двух точек, манхэттенское расстояние между которыми равно \(4\), а следовательно подходящего манхэттенского треугольника не существует.
Примеры
| № | Входные данные | Выходные данные |
|
1
|
6
6 4
3 1
0 0
0 -2
5 -3
3 -5
2 -2
5 4
0 0
0 -2
5 -3
3 -5
2 -2
6 6
3 1
0 0
0 -2
5 -3
3 -5
2 -2
4 4
3 0
0 3
-3 0
0 -3
10 8
2 1
-5 -1
-4 -1
-5 -3
0 1
-2 5
-4 4
-4 2
0 0
-4 1
4 400000
100000 100000
-100000 100000
100000 -100000
-100000 -100000
|
2 6 1
4 3 5
3 5 1
0 0 0
6 1 3
0 0 0
|