Олимпиадный тренинг

Задача . B. Предел

Задача

Даны два многочлена:

P(x) = a₀·xⁿ + a₁·x^n - 1 + ... + a_n - 1·x + a_n и
Q(x) = b₀·x^m + b₁·x^m - 1 + ... + b_m - 1·x + b_m.

Вычислите предел 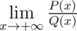$\text{[math]}$ .

Входные данные

В первой строке через пробел записаны два целых числа n и m (0 ≤ n, m ≤ 100) — степени многочленов P(x) и Q(x) соответственно.

Во второй строке через пробел записаны n + 1 целых чисел — коэффициенты многочлена P(x): a₀, a₁, ..., a_n - 1, a_n ( - 100 ≤ a_i ≤ 100, a₀ ≠ 0).

В третьей строке через пробел записаны m + 1 целых чисел — коэффициенты многочлена Q(x): b₀, b₁, ..., b_m - 1, b_m ( - 100 ≤ b_i ≤ 100, b₀ ≠ 0).

Выходные данные

Если предел равен + ∞, выведите «Infinity» (без кавычек). Если предел равен - ∞, выведите «-Infinity» (без кавычек).

Если значение предела равно нулю, выведите «0/1» (без кавычек).

Иначе выведите несократимую дробь — значение предела 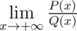$\text{[math]}$ , в формате «p/q» (без кавычек), где p — числитель, q (q > 0) — знаменатель дроби.

Примечание

Рассмотрим все примеры:

$\text{[math]}$
$\text{[math]}$
$\text{[math]}$
$\text{[math]}$
$\text{[math]}$

Об определении и свойствах пределов можно подробнее прочитать по ссылке: http://ru.wikipedia.org/wiki/Предел_функции

Примеры


Infinity
-Infinity
0/1
1/2
-9/5

№	Входные данные	Выходные данные
1	2 1 1 1 1 2 5	Infinity
2	1 0 -1 3 2	-Infinity
3	0 1 1 1 0	0/1
4	2 2 2 1 6 4 5 -7	1/2
5	1 1 9 0 -5 2	-9/5

time 2000 ms
memory 256 Mb
Правила оформления программ и список ошибок при автоматической проверке задач

Статистика успешных решений по компиляторам

	Кол-во
С++	5

Комментарий учителя

Ваш ответ

выберите язык и введите исходный код

Для отправки решения задачи необходимо зарегистрироваться или авторизоваться!

Загруженные файлы

Нет