Это простая версия задачи. Единственное отличие между двумя версиями — ограничение на \(y\). В этой версии \(y = 0\). Вы можете делать взломы, только если обе версии задачи решены.
Бесси получила от своей лучшей подруги Элси праздничный торт в виде правильного многоугольника с \(n\) сторонами. Вершины торта пронумерованы от \(1\) до \(n\) по часовой стрелке. Вы с Бесси собираетесь выбрать некоторые вершины и сделать непересекающиеся разрезы по диагоналям торта так, чтобы концы разрезов входили в множество выбранных вершин.
Бесси хотела бы раздавать только те куски торта, которые являются треугольниками, чтобы всё было честно. Размеры кусков не имеют значения, и весь торт не обязательно должен быть разделен только на треугольники (в торте могут быть куски и других форм, но они не будут учитываться).
Бесси уже выбрала \(x\) вершин, которые могут быть использованы как концы разрезов. Она хочет, чтобы вы выбрали не более \(y\) других вершин так, чтобы количество треугольных кусков торта, которые она может раздать после разрезания, было максимальным.
Какое максимальное количество треугольных кусков торта может раздать Бесси?
Выходные данные
Для каждого набора входных данных выведите одно целое число: максимальное количество непересекающихся треугольных кусков торта, которые она может раздать.
Примечание
В наборах входных данных \(1\), \(2\) и \(3\) можно получить соответственно \(2\), \(6\) и \(2\) непересекающихся треугольных куска торта. Возможные конструкции показаны на следующих рисунках:
Зеленые точки обозначают вершины, которые можно использовать, синие линии — диагонали, которые проводятся, а красные цифры — треугольники, которые подсчитываются.
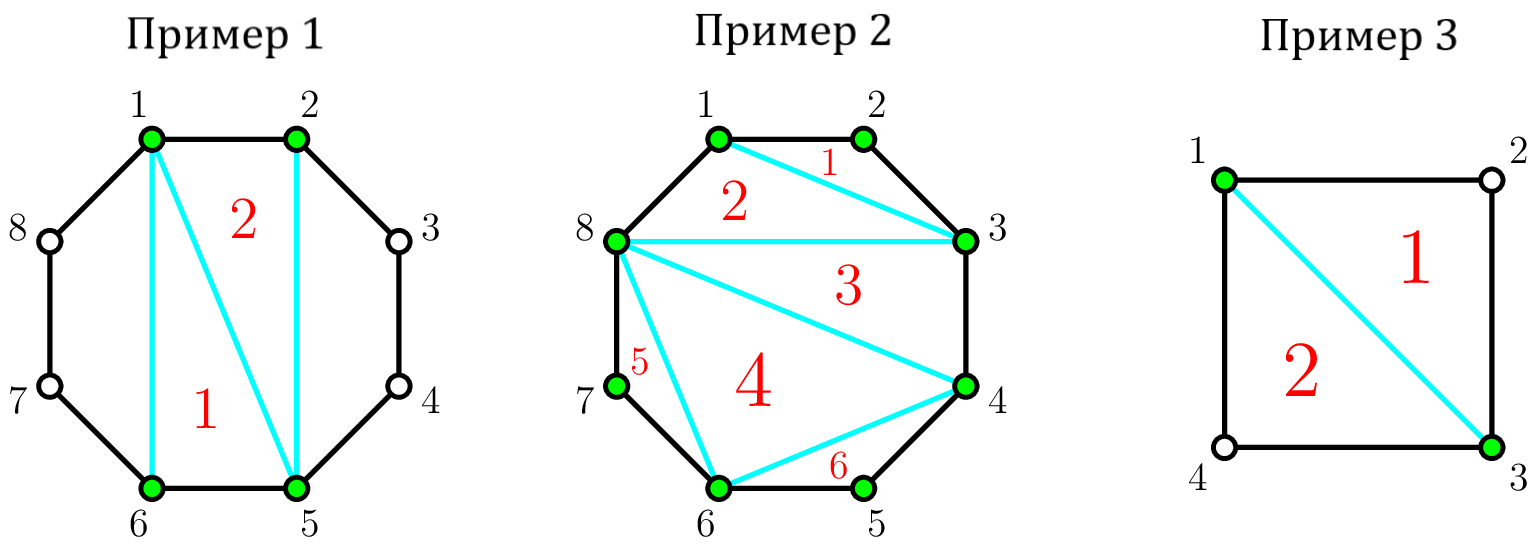
Примеры
| № | Входные данные | Выходные данные |
|
1
|
3
8 4 0
1 6 2 5
8 8 0
1 3 2 5 4 6 7 8
4 2 0
1 3
|
2
6
2
|