Дана таблица размера \(2 \times n\), заполненная нулями и единицами. Пусть число, стоящее на пересечении \(i\)-й строки и \(j\)-го столбца, равно \(a_{ij}\).
В левой верхней клетке \((1, 1)\) находится кузнечик, который может прыгать только на одну клетку вправо или вниз. Ему нужно добраться до правой нижней клетки \((2, n)\). Рассмотрим бинарную строку длины \(n+1\), состоящую из чисел, записанных в клетках пути, без изменения их относительного порядка.
Вам необходимо:
- Найти лексикографически наименьшую\(^\dagger\) строку, которую можно получить, выбрав один из доступных путей;
- Найти количество путей, которые дают эту лексикографически наименьшую строку.
\(^\dagger\) Если строки \(s\) и \(t\) имеют равную длину, то строка \(s\) лексикографически меньше строки \(t\), если и только если в первой позиции, где \(s\) и \(t\) различны, в строке \(s\) элемент меньше, чем соответствующий элемент в \(t\).
Выходные данные
Для каждого набора входных данных выведите:
- Лексикографически наименьшую строку, которую можно получить;
- Число путей, дающих эту строку.
Примечание
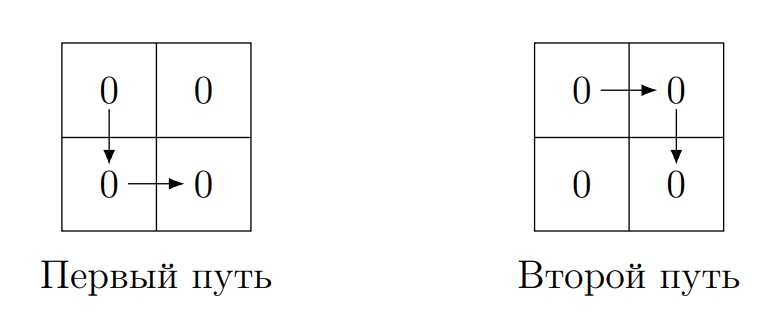
В первом наборе входных данных лексикографически наименьшей строкой является \(\mathtt{000}\). Есть два пути, движение по которым даст эту строку:
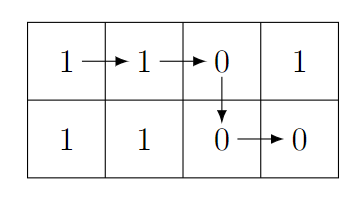
Во втором наборе входных данных лексикографически наименьшей строкой является \(\mathtt{11000}\). Существует всего один путь, дающий такую строку:
Примеры
| № | Входные данные | Выходные данные |
|
1
|
3
2
00
00
4
1101
1100
8
00100111
11101101
|
000
2
11000
1
001001101
4
|