Мир представляет собой прямоугольную таблицу с \(n\) строками и \(m\) столбцами. Строки нумеруются \(0, 1, \ldots, n-1\), а столбцы нумеруются \(0, 1, \ldots, m-1\). В этом мире столбцы циклические (т.е. верхние и нижние ячейки в каждом столбце смежны). Ячейка в \(i\)-й строке и \(j\)-м столбце (\(0 \le i < n, 0 \le j < m\)) обозначается как \((i,j)\).
В момент времени \(0\) ячейка \((i,j)\) (где \(0 \le i < n, 0 \le j < m\)) содержит либо камень, либо ничего. Состояние ячейки \((i,j)\) можно описать с помощью целого числа \(a_{i,j}\):
- Если \(a_{i,j} = 1\), в \((i,j)\) есть камень.
- Если \(a_{i,j} = 0\), в \((i,j)\) ничего нет.
В результате подземных толчков от землетрясения, столбцы следуют за движениями тектонических плит: каждый столбец циклически двигается вверх со скоростью \(1\) ячейка за единицу времени. Формально, для некоторых \(0 \le i < n, 0 \le j < m\), если в данный момент времени в \((i,j)\) есть камень, он переместится из \((i, j)\) в \((i - 1, j)\) (или в \((n - 1, j)\), если \(i=0\)).
Робот по имени RT изначально находится в позиции \((0,0)\). Ему нужно добраться до \((n-1,m-1)\) для проведения операции спасения от землетрясения (в правый нижний угол поля). Подземные толчки не изменяют положения робота, они только изменяют положение камней в мире.
Пусть текущее положение RT имеет координаты \((x,y)\) (\(0 \le x < n, 0 \le y < m\)), он может выполнить следующие операции:
- Перейти на одну ячейку циклически вверх, т.е. из \((x,y)\) в \(((x+n-1) \bmod n, y)\) за \(1\) единицу времени.
- Перейти на одну ячейку циклически вниз, т.е. из \((x,y)\) в \(((x+1) \bmod n, y)\) за \(1\) единицу времени.
- Перейти на одну ячейку вправо, т.е. из \((x,y)\) в \((x, y+1)\) за \(1\) единицу времени. (RT может выполнить эту операцию только если \(y < m-1\).)
Обратите внимание, что RT не может ни двигаться влево с помощью этих операций, ни оставаться на месте.
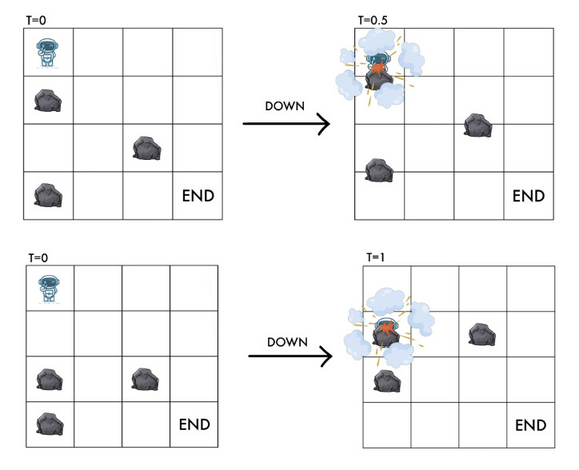
К сожалению, RT взорвется при столкновении с камнем. Поэтому, когда RT находится в \((x,y)\) и есть камень в \(((x+1) \bmod n, y)\) или \(((x+2) \bmod n, y)\), RT не может двигаться вниз, иначе он столкнется с камнем.
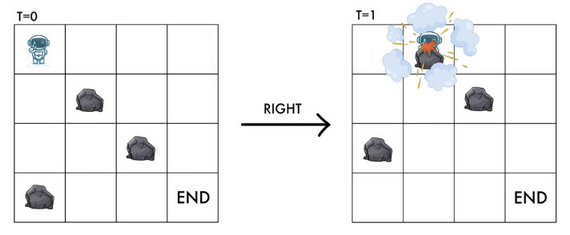
Аналогично, если \(y+1 < m\) и есть камень в \(((x+1) \bmod n, y+1)\), RT не может двигаться вправо, иначе он столкнется с камнем.
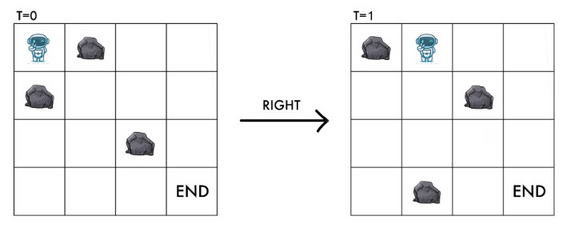
Стоит отметить, что если на клетках \((x \bmod n, y+1)\) и \(((x+1) \bmod n, y)\) находится камень, RT всё равно может безопасно перейти вправо.
Найдите минимальное количество времени, которое RT нужно, чтобы добраться до \((n-1,m-1)\) без столкновения с камнями. Если это невозможно, выведите \(-1\).