Однажды непутёвый озорной стрелок по имени Шел попал на прямоугольное поле размером \(n \times m\), разбитое на единичные квадратики. В каждой из клеток либо стоит мишень, либо нет.
С собой у Шел оказался только счастливый дробовик, из которого можно выстрелить в одну из четырёх сторон: вправо-вниз, влево-вниз, влево-вверх или вправо-вверх. При выстреле дробовик поражает все мишени в выбранном направлении, Манхэттенское расстояние до которых не больше фиксированной для дробовика константы \(k\). Манхэттенское расстояние между двумя точками \((x_1, y_1)\) и \((x_2, y_2)\) равно \(|x_1 - x_2| + |y_1 - y_2|\).
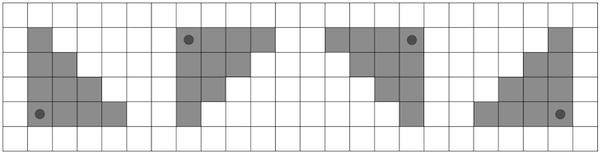Возможные области поражения для \(k = 3\). Цель Шел — поразить как можно большее количество мишеней. Помогите ему, пожалуйста, найти это значение.
Выходные данные
Для каждого набора входных данных в отдельной строке выведите одно число, которое равно максимально возможному количеству поражённых мишеней за один выстрел.
Примечание
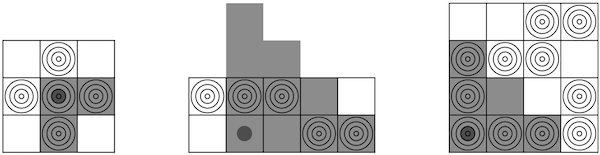
Возможные оптимальные выстрелы для примеров из условия:
Примеры
| № | Входные данные | Выходные данные |
|
1
|
4
3 3 1
.#.
###
.#.
2 5 3
###..
...##
4 4 2
..##
###.
#..#
####
2 1 3
#
#
|
3
4
5
2
|