Единственное отличие двух версий этой задачи состоит в ограничении на \(q\). Вы можете делать взломы, только если обе версии задачи решены.
Томас плавает вокруг острова, окружённого океаном. Океан и остров можно представить в виде таблицы с \(n\) строками и \(m\) столбцами. Строки пронумерованы от \(1\) до \(n\) сверху вниз, а столбцы пронумерованы от \(1\) до \(m\) слева направо. Позицию клетки в строке \(r\) и в столбце \(c\) обозначим как \((r, c)\). Ниже приведен пример допустимой таблицы.
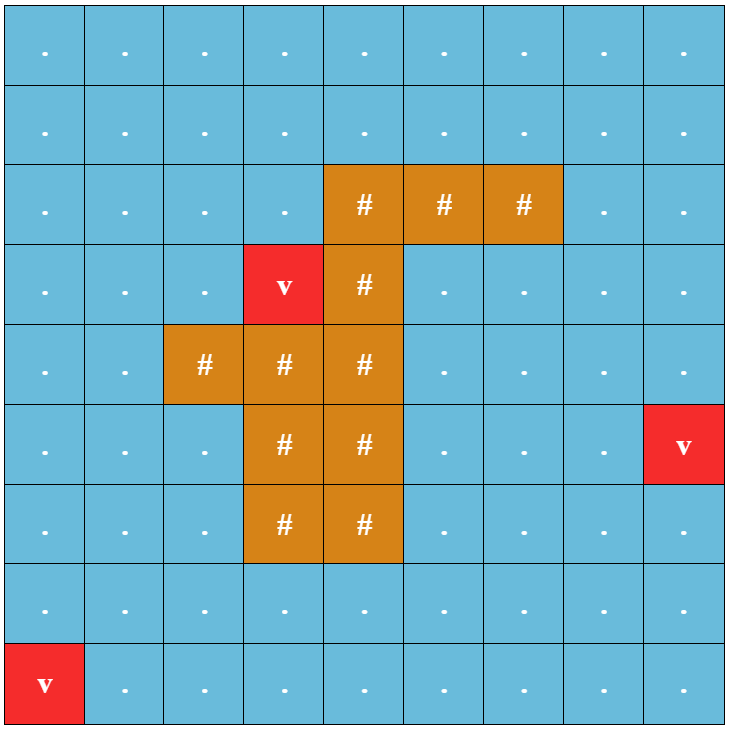 Пример допустимой таблицы
Пример допустимой таблицы Существует три типа клеток: остров, океан и подводный вулкан. Клетки, представляющие остров, отмечены символом '#', клетки, представляющие океан, отмечены символом '.', а клетки, представляющие подводный вулкан, отмечены символом 'v'. Гарантируется, что есть хотя бы одна клетка острова и хотя бы одна клетка подводного вулкана. Также гарантируется, что множество всех клеток острова образует единую связную компоненту\(^{\dagger}\), и множество всех клеток океана и подводных вулканов также образует единую связную компоненту. Кроме того, гарантируется, что на краю таблицы (то есть, в строке \(1\), в строке \(n\), в столбце \(1\) и в столбце \(m\)) нет клеток острова.
Определим круговой маршрут, проходимый Томасом, начинающийся в клетке \((x, y)\), как путь, который удовлетворяет следующим условиям:
- Путь начинается и заканчивается в клетке \((x, y)\).
- Если Томас находится в клетке \((i, j)\), то он может перейти в клетки \((i+1, j)\), \((i-1, j)\), \((i, j-1)\) и \((i, j+1)\), при условии, что клетка, в которую он переходит, является клеткой океана или подводного вулкана и находится внутри таблицы. Обратите внимание, что Томасу разрешается посещать одну и ту же клетку несколько раз за один круговой маршрут.
- Путь должен обойти остров и полностью его окружить. Некоторый путь \(p\) полностью окружает остров, если невозможно добраться от клетки острова до клетки на границе таблицы, перемещаясь только в соседние по стороне или диагонали клетки, не посещая при этом клетку на пути \(p\). На изображении ниже путь, начинающийся в \((2, 2)\), приходящий в \((1, 3)\) и возвращающийся в \((2, 2)\) в обратную сторону, не полностью окружает остров и не считается круговым маршрутом.
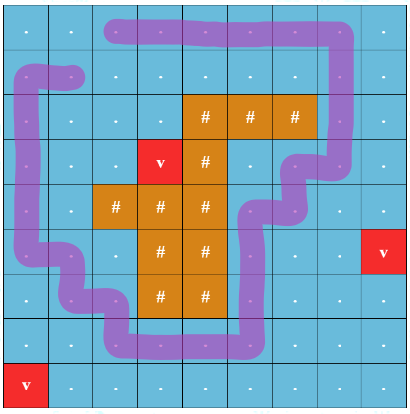 Пример пути, который не полностью окружает остров
Пример пути, который не полностью окружает остров Безопасность кругового маршрута — это минимальное манхэттенское расстояние\(^{\ddagger}\) от клетки на круговом маршруте до подводного вулкана (обратите внимание, что наличие клеток острова не влияет на это расстояние).
У вас есть \(q\) запросов. Запрос можно представить как \((x, y)\), и для каждого запроса вы хотите найти максимальную безопасность кругового маршрута, начинающегося в \((x, y)\). Гарантируется, что \((x, y)\) является клеткой океана или подводного вулкана.
\(^{\dagger}\)Множество клеток образует единую связную компоненту, если из любой клетки этого множества можно добраться до любой другой клетки этого множества, перемещаясь только по клеткам этого множества, каждый раз переходя в клетку с общей стороной.
\(^{\ddagger}\)Манхэттенское расстояние между клетками \((r_1, c_1)\) и \((r_2, c_2)\) равно \(|r_1 - r_2| + |c_1 - c_2|\).
Примечание
Для первого примера на изображении ниже показан оптимальный круговой маршрут, начинающийся в \((1, 1)\). Безопасность кругового маршрута равна \(3\), так как минимальное манхэттенское расстояние от клетки на круговом маршруте до подводного вулкана равно \(3\).
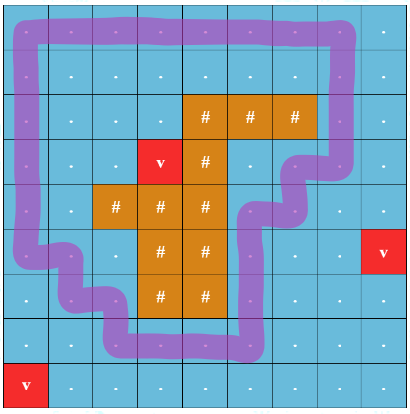 Пример оптимального кругового маршрута
Пример оптимального кругового маршрута В четвёртом примере помните, что Томасу разрешается посещать одну и ту же клетку несколько раз за один круговой маршрут. Например, это необходимо для кругового маршрута, начинающегося в \((7, 6)\).