У Кристины есть матрица размера \(n\) на \(n\), заполненная строчными латинскими буквами. При этом значение \(n\) четное.
Ей хочется изменить некоторые символы так, чтобы ее матрица стала идеальным квадратом. Назовём матрицу идеальным квадратом, если после одного поворота на \(90^\circ\) по часовой стрелке она не изменится.
Пример поворота матрицы на \(90^\circ\):
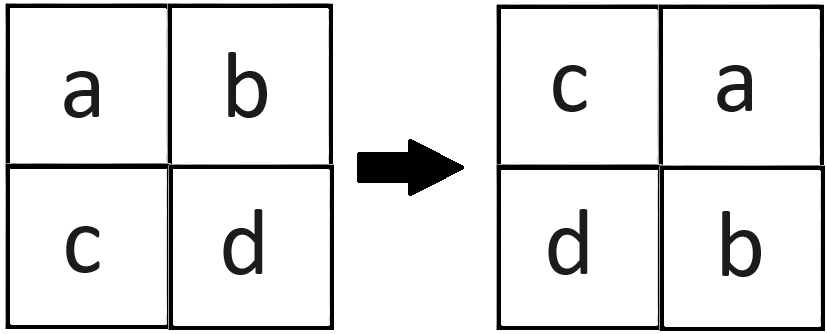
За одну операцию Кристина может выбрать любой элемент и заменить его значение на следующий символ в алфавите. Если символ равен «z», то его значение не изменится.
Найдите минимальное количество операций, которое необходимо применить для того, чтобы матрица стала идеальным квадратом.
Например, если матрица размера \(4\) на \(4\) выглядит так:
\(\)\matrix{ a & b & b & a \cr b & c & \textbf{b} & b \cr b & c & c & b\cr a & b & b & a \cr }\(\)
то в ней достаточно применить \(1\) операцию к букве b, выделенной жирным.
Выходные данные
В отдельной строке для каждого набора входных данных выведите единственное число: минимальное количество операций, которое необходимо применить, чтобы у Кристины получился идеальный квадрат.