Вы любите рыб, поэтому решили построить аквариум. У вас есть кусок коралла, состоящий из \(n\) колонн, \(i\)-я из которых имеет высоту \(a_i\) единиц. Затем вы построите вокруг коралла аквариум следующим образом:
- Выберите целое число \(h \geq 1\) — высоту аквариума. Постройте стены высотой \(h\) с обеих сторон аквариума.
- Затем заполните аквариум водой так, чтобы высота каждой колонны была равна \(h\), если только коралл не выше \(h\); в этом случае в эту колонну вода добавляться не должна.
Например, с
\(a=[3,1,2,4,6,2,5]\) и высотой
\(h=4\), вы потратите в общей сложности
\(w=8\) единиц воды, как показано на рисунке.
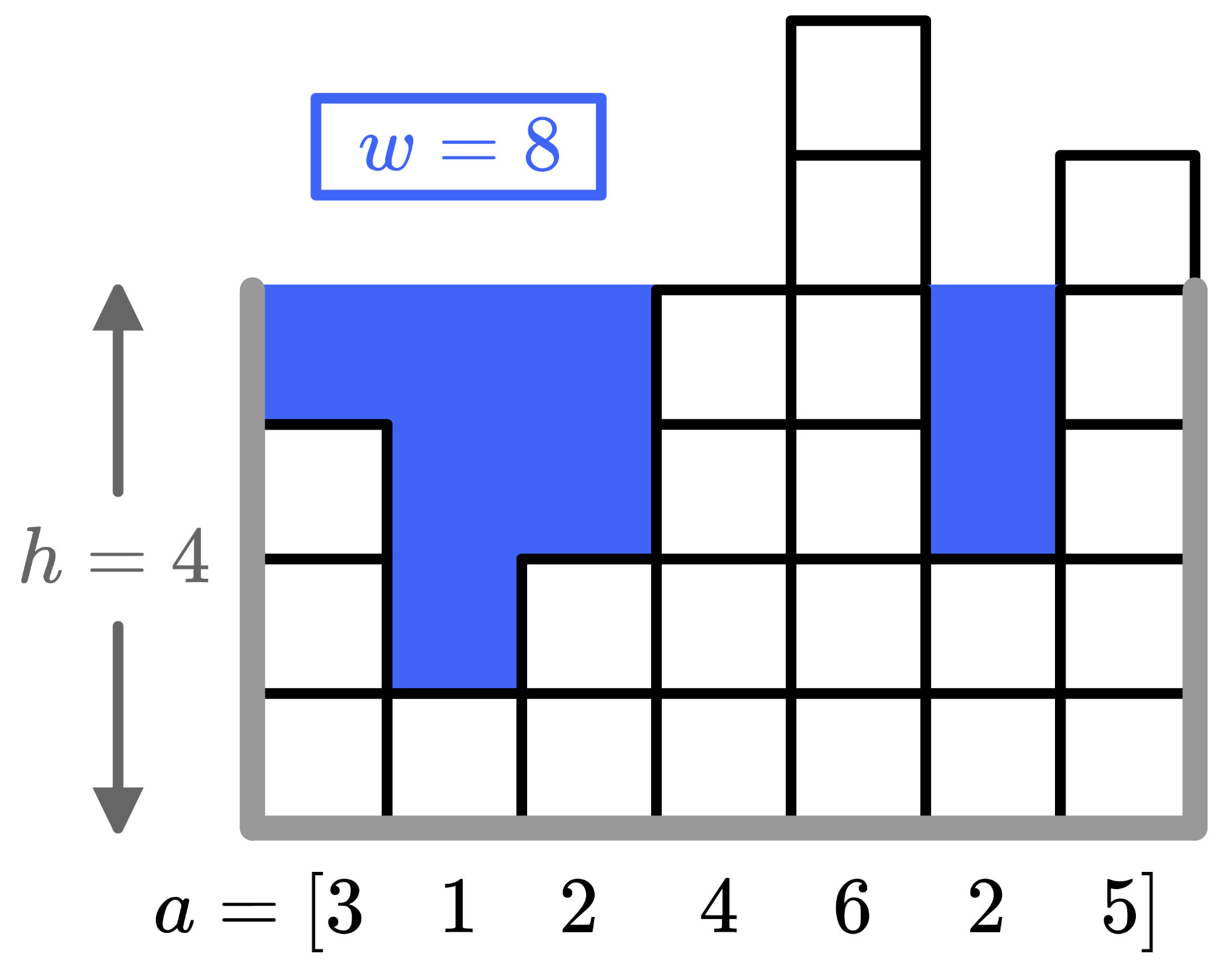
Вы можете использовать не более
\(x\) единиц воды для заполнения аквариума, но вы хотите построить наибольший возможный аквариум. Какое наибольшее значение
\(h\) вы можете выбрать?
Выходные данные
Для каждого набора входных данных выведите одно положительное целое число \(h\) (\(h \geq 1\)) — максимальную высоту аквариума, для заполнения которого вам потребуется не более \(x\) единиц воды.
Можно доказать, что при таких ограничениях всегда существует такое значение \(h\).
Примечание
Первый пример изображен в условии. С \(h=4\) нам потребуется \(8\) единиц воды, но если увеличить \(h\) до \(5\), нам потребуется \(13\) единиц воды, что больше, чем \(x=9\). Поэтому оптимальное значение \(h=4\).
Во втором примере случае мы можем выбрать \(h=4\) и добавить \(3\) единицы к каждой колонне, используя в общей сложности \(9\) единиц воды. Можно показать, что это оптимально.
В третьем примере случае мы можем выбрать \(h=2\) и использовать всю нашу воду, поэтому это оптимально.
Примеры
| № | Входные данные | Выходные данные |
|
1
|
5
7 9
3 1 2 4 6 2 5
3 10
1 1 1
4 1
1 4 3 4
6 1984
2 6 5 9 1 8
1 1000000000
1
|
4
4
2
335
1000000001
|