Вам даны целые числа \(n\) и \(m\). Заполните таблицу размером \(n\) на \(m\) целыми числами от \(1\) до \(n\cdot m\) таким образом, чтобы для любых двух соседних клеток сетки модуль разности значений в этих клетках не был простым числом. Две клетки в таблице считаются соседними, если они имеют общую сторону.
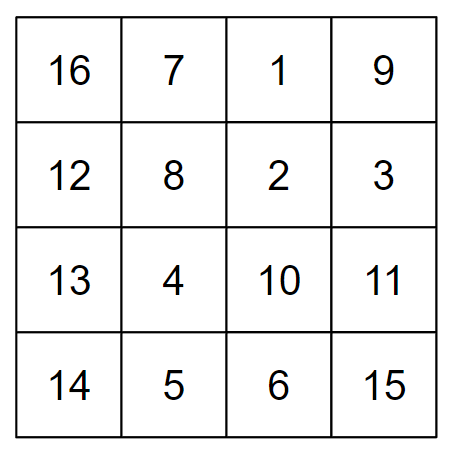
Можно показать, что при заданных ограничениях решение всегда существует.
Выходные данные
Для каждого набора входных данных выведите \(n\) строк по \(m\) целых чисел в каждой, представляющих итоговую таблицу. Каждое число от \(1\) до \(n\cdot m\) должно появиться в таблице ровно один раз.
Дополнительные пробелы и пустые строки в приведенном ниже примере вывода присутствуют только для удобства чтения и не являются обязательными.
Если существует несколько решений, выведите любое из них.
Примечание
Первый пример соответствует картинке выше. Единственными абсолютными разностями между соседними элементами в этой таблице являются числа \(1\), \(4\), \(6\), \(8\) и \(9\), ни одно из которых не является простым.
Примеры
| № | Входные данные | Выходные данные |
|
1
|
3
4 4
5 7
6 4
|
16 7 1 9
12 8 2 3
13 4 10 11
14 5 6 15
29 23 17 9 5 6 2
33 27 21 15 11 7 1
32 31 25 19 20 16 10
26 30 24 18 14 8 4
35 34 28 22 13 12 3
2 3 7 11
8 9 1 10
17 13 5 4
18 14 6 12
19 23 15 21
20 24 16 22
|