Альперен стоит в точке \((0,0)\). Ему дана строка \(s\) длины \(n\) и он производит \(n\) перемещений: \(i\)-е перемещение происходит так:
- если \(s_i = \texttt{L}\), он перемещается на одну клетку влево;
- если \(s_i = \texttt{R}\), он перемещается на одну клетку вправо;
- если \(s_i = \texttt{U}\), он перемещается на одну клетку вверх;
- если \(s_i = \texttt{D}\), он перемещается на одну клетку вниз.
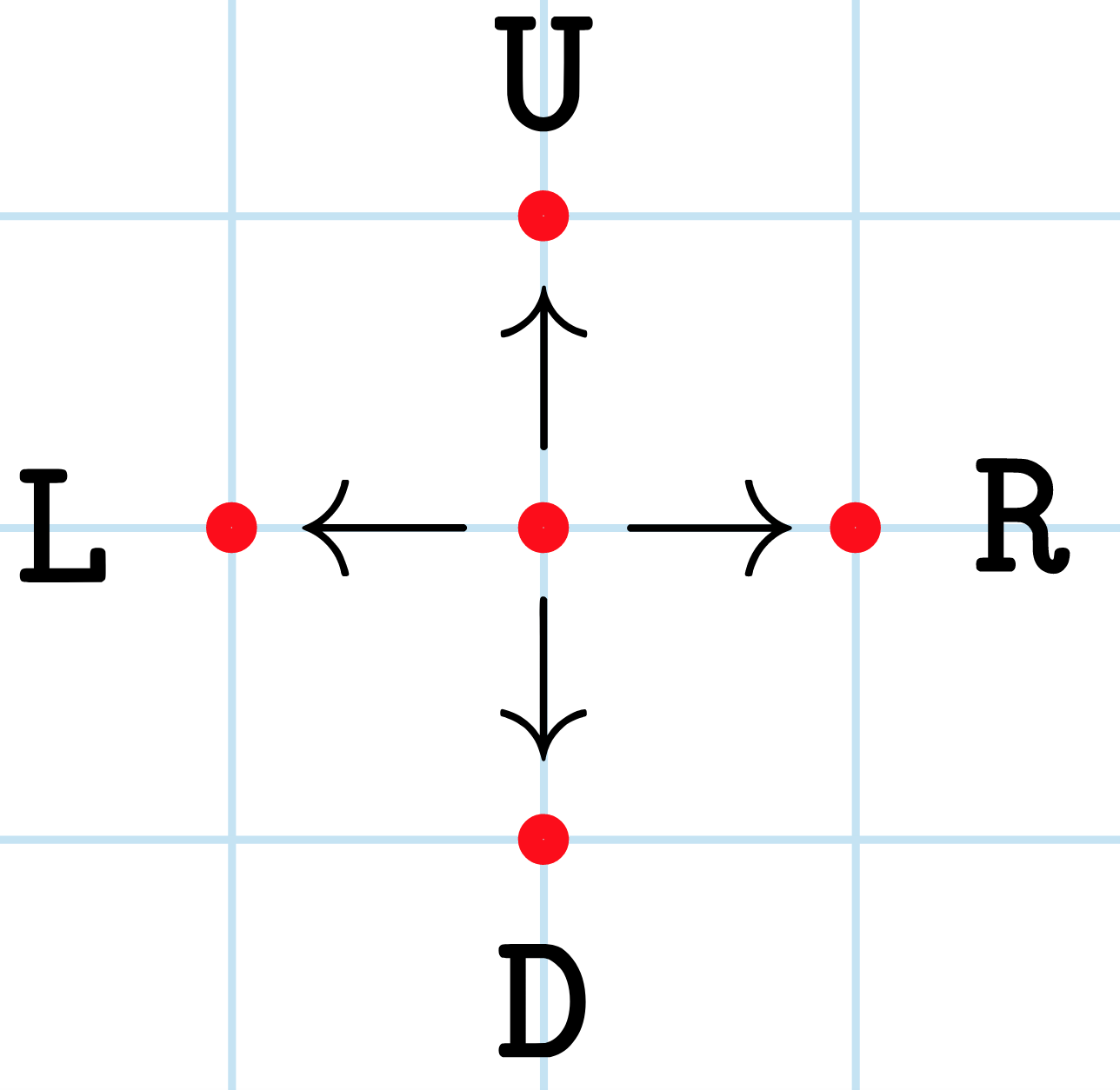Если Альперен начинает в точке в центре, он может сделать четыре различных перемещения, как показано на рисунке. В точке
\((1,1)\) находится конфета (то есть на одну клетку вверх и на одну клетку вправо от начальной точки, в которой находится Альперен). Определите, доберется ли Альперен когда-нибудь до конфеты.
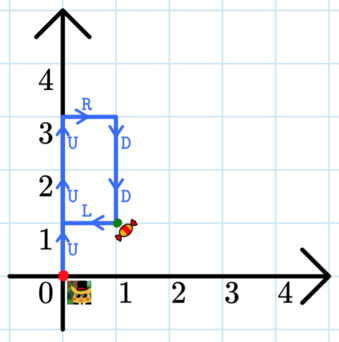Alperen's path in the first test case. Выходные данные
Для каждого набора входных данных выведите «YES» (без кавычек), если Альперен доберется до конфеты, в противном случае, выведите «NO» (без кавычек).
Вы можете выводить ответ в любом регистре (например, строки «yEs», «yes», «Yes» и «YES» будут приняты как положительный ответ).
Примечание
В первом наборе входных данных Альперен следует по пути \(\)(0,0) \overset{\texttt{U}}{\to} (0,1) \overset{\texttt{U}}{\to} (0,2) \overset{\texttt{U}}{\to} (0,3) \overset{\texttt{R}}{\to} (1,3) \overset{\texttt{D}}{\to} (1,2) \overset{\texttt{D}}{\to} \color{green}{\mathbf{(1,1)}} \overset{\texttt{L}}{\to} (0,1).\(\) Обратите внимание, что Альперену не обязательно находится в точке \((1,1)\) в конце своего пути, ему достаточно оказаться там хотя бы раз за весь путь.
Во втором наборе Альперен следует по пути \(\)(0,0) \overset{\texttt{U}}{\to} (0,1) \overset{\texttt{R}}{\to} \color{green}{\mathbf{(1,1)}}.\(\)
В третьем наборе Альперен следует по пути \(\)(0,0) \overset{\texttt{R}}{\to} (1,0) \overset{\texttt{R}}{\to} (2,0) \overset{\texttt{R}}{\to} (3,0) \overset{\texttt{U}}{\to} (3,1) \overset{\texttt{U}}{\to} (3,2) \overset{\texttt{D}}{\to} (3,1) \overset{\texttt{D}}{\to} (3,0) \overset{\texttt{D}}{\to} (3,-1).\(\)
В четвертом наборе Альперен следует по пути \(\)(0,0) \overset{\texttt{L}}{\to} (-1,0) \overset{\texttt{L}}{\to} (-2,0) \overset{\texttt{L}}{\to} (-3,0).\(\)