Олимпиадный тренинг

Задача . G. Игра века

Задача

Темы: графы Конструктив кратчайшие пути *3000

Время пришло, MKnez и Балтик должны наконец-то провести Игры века. Для этого они построили деревню для размещения всех участников.

Деревня имеет вид равностороннего треугольника, ограниченного тремя дорогами длины $n$. Она разделена на $n^2$ меньших равносторонних треугольников со стороной $1$ с помощью $3n-3$ дополнительных дорог, параллельных сторонам, см. рисунок для $n=3$. Каждая из $3n$ дорог состоит из нескольких (возможно, $1$) участков дороги длины $1$, соединяющих соседние перекрестки.

$\text{[math]}$

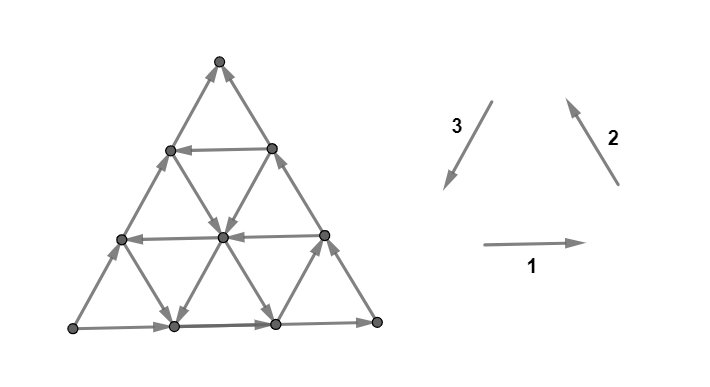
Для всех $3n$ дороги уже выбраны направления (то есть, для каждой дороги выбрано одно и то же направление для всех ее участков). Транспорт может двигаться по участкам дорог только в выбранном направлении (т. е. дороги односторонние).

Ваша задача — внести поправки в план движения так, чтобы от каждого перекрестка можно было доехать до любого другого. А именно, вы можете изменять направление движения на любом участке дороги длины $1$. Чему равно минимальное количество участков дорог, на которых нужно изменить направление?

Входные данные

Каждый тест состоит из нескольких наборов входных данных. В первой строке находится одно целое число $t$ ($1 \leq t \leq 10\,000$) — количество наборов входных данных. Далее следует описание наборов входных данных.

Первая строка каждого набора входных данных содержит целое положительное число $n$ ($1\leq n\leq 10^5$) — размер стороны треугольной деревни.

Далее следуют три строки, каждая из которых содержит бинарную строку длины $n$, описывающую направления движения на дорогах.

$i$-я из этих строк содержит бинарную строку $s_i$ длины $n$, описывающую направления на дорогах, параллельных дороге $i$ на рисунке выше. А именно, $j$-й символ $s_i$ равен «1», если $j$-я кратчайшая дорога (параллельная дороге $i$ на рисунке) имеет такое же направление, как дорога $i$ на рисунке, и «0», если ее направление противоположное. Таким образом, первый символ $s_i$ описывает направление на дороге из $1$ участка, а последний символ описывает направление на дороге из $n$ участков.

Гарантируется, что сумма значений $n$ по всем наборам входных данных не превосходит $10^5$.

Выходные данные

Для каждого набора входных данных выведите минимальное количество участков дороги, на которых нужно изменить направление движения.

Примечание

Первый пример показан на рисунке в условии. Существует несколько решений, изменяющих направление на ровно $2$ участках дорог, но изменение направления только на $1$ участке дороги не может привести к тому, что от каждого перекрестка можно добраться до любого другого. Одно из возможных решений показано на рисунке ниже, измененные участки дорог показаны синим.

$\text{[math]}$

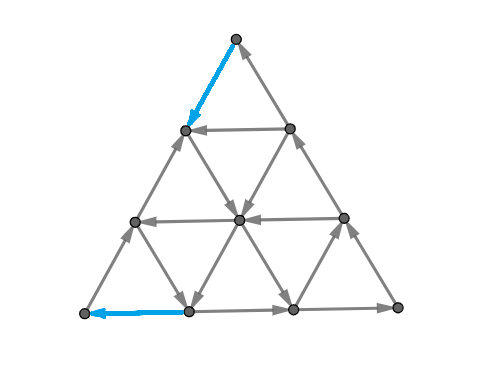
Во втором примере ответ равен $0$, потому что уже в изначальной конфигурации можно от каждого перекрестка добраться до любого другого.

Примеры

№	Входные данные	Выходные данные
1	3 3 001 001 010 1 0 0 0 3 111 011 100	2 0 3

time 2000 ms
memory 256 Mb
Правила оформления программ и список ошибок при автоматической проверке задач

Статистика успешных решений по компиляторам

	Кол-во
С++ Mingw-w64	5

Комментарий учителя

Ваш ответ

выберите язык и введите исходный код

Для отправки решения задачи необходимо зарегистрироваться или авторизоваться!

Загруженные файлы

Нет