Косия и Махиру наслаждаются зимним фестивалем. Улицы зимнего фестиваля можно представить как неориентированный граф-сетку размера \(n \times n\). Формально, множество вершин определяется как \(\{(i,j) \; | \; 1 \leq i,j\leq n \}\), и две вершины \((i_1,j_1)\) и \((i_2,j_2)\) соединены ребром только тогда когда \(|i_1-i_2|+|j_1-j_2|=1\).
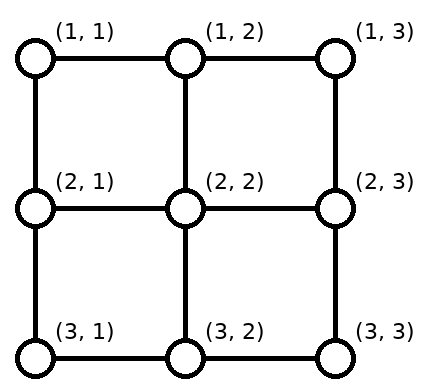Граф размера \(n = 3\). Косия и Махиру планируют посетить зимний фестиваль, проехав по \(2n\) маршрутам. Сами маршруты еще не определены, но начала и концы маршрутов уже известны:
- На \(i\)-м маршруте они начнут из вершины \((1, i)\) и закончат в вершине \((n, p_i)\), где \(p\) — перестановка длины \(n\).
- На \((i+n)\)-м маршруте они начнут из вершины \((i, 1)\) и закончат в вершине \((q_i, n)\), где \(q\) — перестановка длины \(n\).
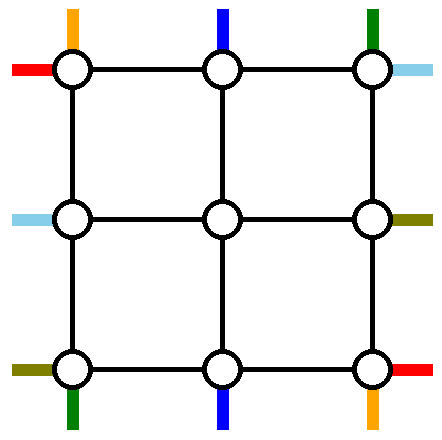Граф размера \(n = 3\), одинаковыми цветами показаны начала и концы одного маршрута для \(p = [3, 2, 1]\) и \(q = [3, 1, 2]\). Ваша задача — создать схему маршрутов, то есть выбрать \(2n\) путей таких, что каждый путь соединяет заданные начало и конец. Определим загрузку ребра как количество раз, которое это ребро используется (суммарно в обе стороны) в схеме маршрутов. Чтобы Косия и Махиру не слишком скучали от проезда одних и тех же ребер, найдите схему маршрутов, минимизирующую максимальную загрузку среди всех ребер.
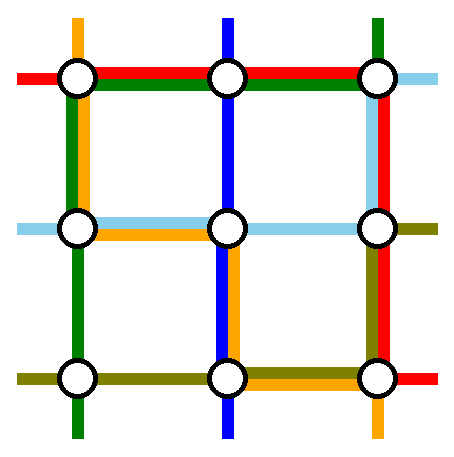Пример решения. Максимальная загрузка равна \(2\), что оптимально для этого случая. Выходные данные
Выведите \(2n\) строк, каждая из которых описывает маршрут.
Первые \(n\) строк должны описывать маршруты, идущие сверху вниз. \(i\)-я строка должна описывать маршрут, начинающийся в вершине \((1, i)\) и заканчивающийся в вершине \((n, p_i)\).
Следующие \(n\) строк должны описывать маршруты, идущие слева направо. \((i+n)\)-я строка должна описывать маршрут, начинающийся в вершине \((i, 1)\) и заканчивающийся в вершине \((q_i, n)\).
Каждая строка, описывающая маршрут, должна начинаться с числа \(k\) (\(2 \le k \le 10^5\)) — количество вершин, через которые проходит маршрут, включая начальную и конечную. Далее выведите все вершины, через которые проходит маршрут, по порядку. Иными словами, если маршрут выглядит как \((x_1, y_1) \rightarrow (x_2, y_2) \rightarrow \dots \rightarrow (x_k, y_k)\), то выведите \(k~x_1~y_1~x_2~y_2 \ldots x_k~y_k\). Обратите внимание, что \(|x_i-x_{i+1}|+|y_i-y_{i+1}| = 1\) должно выполняться для всех \(1 \le i < k\).
Если существует несколько решений, минимизирующих максимальную загрузку, выведите любое.
Примечание
Первый пример соответствует рисункам из условия задачи.
Примеры ответов для примеров \(2\) и \(3\) показаны ниже:
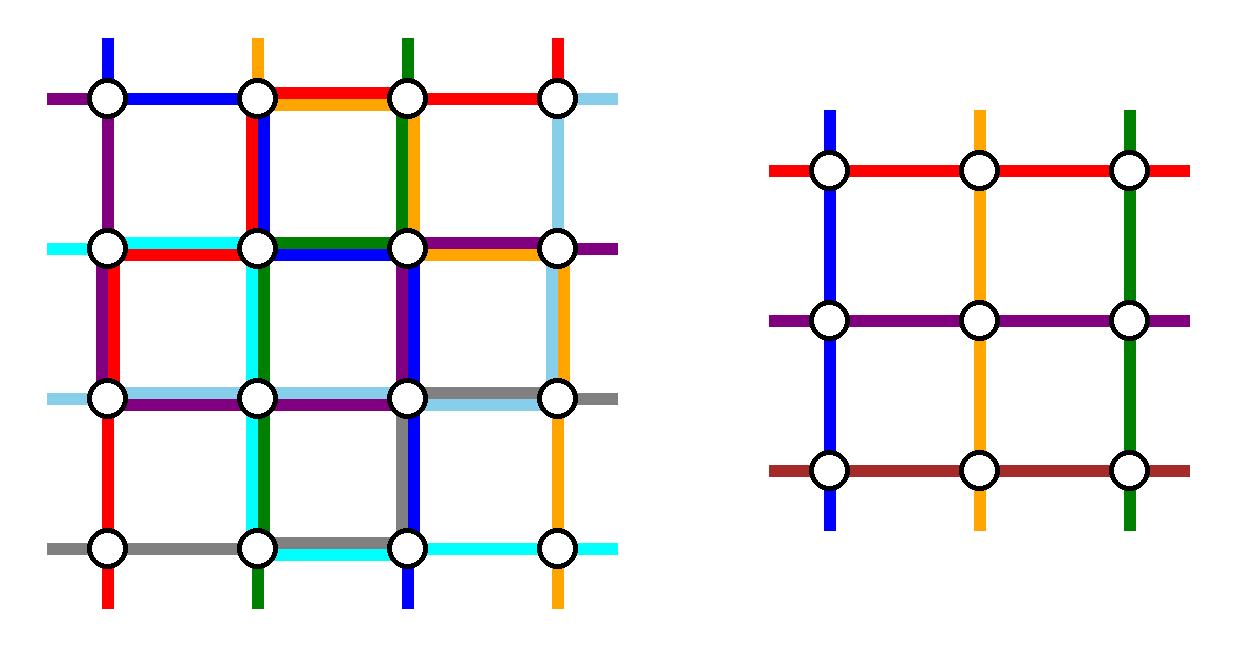Примеры ответов для примеров \(2\) и \(3\). Максимальная загрузка равна соответственно \(2\) и \(1\).
Примеры
| № | Входные данные | Выходные данные |
|
1
|
3
3 2 1
3 1 2
|
5 1 1 2 1 2 2 3 2 3 3
3 1 2 2 2 3 2
5 1 3 1 2 1 1 2 1 3 1
5 1 1 1 2 1 3 2 3 3 3
4 2 1 2 2 2 3 1 3
4 3 1 3 2 3 3 2 3
|
|
2
|
4
3 4 2 1
2 4 1 3
|
6 1 1 1 2 2 2 2 3 3 3 4 3
6 1 2 1 3 2 3 2 4 3 4 4 4
5 1 3 2 3 2 2 3 2 4 2
7 1 4 1 3 1 2 2 2 2 1 3 1 4 1
7 1 1 2 1 3 1 3 2 3 3 2 3 2 4
6 2 1 2 2 3 2 4 2 4 3 4 4
6 3 1 3 2 3 3 3 4 2 4 1 4
5 4 1 4 2 4 3 3 3 3 4
|
|
3
|
3
1 2 3
1 2 3
|
3 1 1 2 1 3 1
3 1 2 2 2 3 2
3 1 3 2 3 3 3
3 1 1 1 2 1 3
3 2 1 2 2 2 3
3 3 1 3 2 3 3
|