Давайте назовем упорядоченную пару вершин \((u, v)\) в ориентированном графе однонаправленный если \(u \neq v\), существует путь от \(u\) до \(v\), и не существует пути от \(v\) до \(u\).
Ориентированный граф называется \(p\)-достижимым, если он содержит ровно \(p\) упорядоченных пар вершин \((u, v)\) таких, что \(u < v\), \(u\) и \(v\) достижимы друг из друга. Найдите минимальное количество вершин, необходимое для создания \(p\)-достижимого ориентированного.
Еще, среди всех \(p\)-достижимых ориентированных графов с минимальным числом вершин, пусть \(G\) обозначает граф, который максимизирует количество однонаправленных пар вершин. Найдите это число.
Выходные данные
Выведите одну строку, содержащую два целых числа — минимальное количество вершин, необходимое для создания \(p\)-достижимого ориентированного графа, и максимальное количество однонаправленных пар вершин среди всех таких \(p\)-достижимых ориентированных графов с минимальным количеством вершин.
Примечание
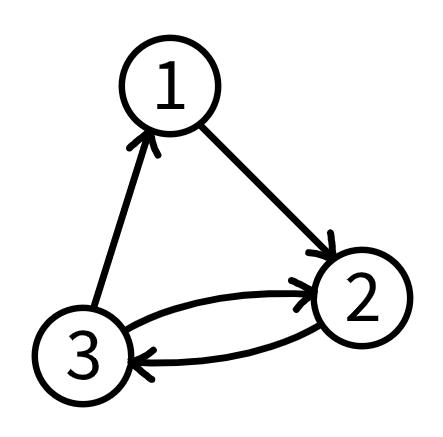
В первом примере минимальное количество вершин, необходимое для создания \(3\)-достижимого ориентированного графа это \(3\). Среди всех \(3\)-достижимых ориентированных графов с \(3\) вершинами, следующий граф \(G\) является одним из графиков с максимальным количеством однонаправленных пар вершин, который является \(0\).
Примеры
| № | Входные данные | Выходные данные |
|
1
|
3
|
3 0
|
|
2
|
4
|
5 6
|
|
3
|
0
|
0 0
|