Вы живете на бесконечной плоскости с введенными декартовыми координатами. За один шаг вы можете пойти в одну из четырех соседних точек (налево, направо, наверх или вниз).
Более формально, если вы стоите в точке \((x, y)\), вы можете:
- пойти налево и переместиться в точку \((x - 1, y)\), или
- пойти направо и переместиться в точку \((x + 1, y)\), или
- пойти наверх и переместиться в точку \((x, y + 1)\), или
- пойти вниз и переместиться в точку \((x, y - 1)\).
На плоскости расположены \(n\) коробок. \(i\)-я из этих коробок находится в точке с координатами \((x_i,y_i)\). Гарантируется, что коробки находятся либо на оси \(x\), либо на оси \(y\), то есть \(x_i=0\), или \(y_i=0\).
Вы можете подобрать коробку если находитесь в одной точке с ней. Найдите минимальное число шагов, необходимое, чтобы собрать все коробки, при условии что вы начинаете и заканчиваете в точке \((0,0)\).
Примечание
В первом примере одна из оптимальных последовательностей шагов показана ниже.
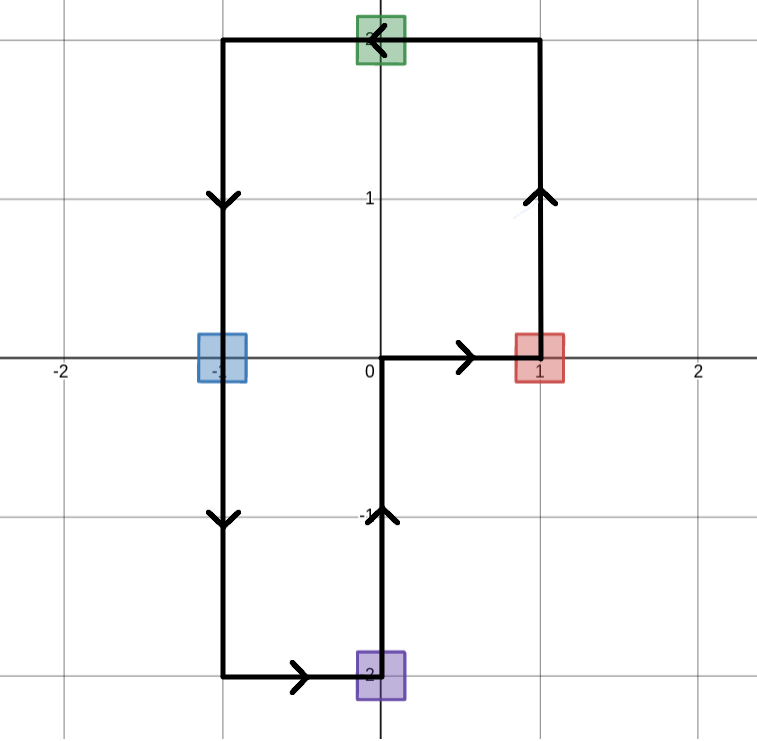 \(\)(0,0) \to (1,0) \to (1,1) \to (1, 2) \to (0,2) \to (-1,2) \to (-1,1) \to (-1,0) \to (-1,-1) \to (-1,-2) \to (0,-2) \to (0,-1) \to (0,0)\(\)
\(\)(0,0) \to (1,0) \to (1,1) \to (1, 2) \to (0,2) \to (-1,2) \to (-1,1) \to (-1,0) \to (-1,-1) \to (-1,-2) \to (0,-2) \to (0,-1) \to (0,0)\(\) Во втором примере одна из оптимальных последовательностей шагов показана на рисунке ниже.
 \(\)(0,0) \to (0,1) \to (0,2) \to (-1, 2) \to (-2,2) \to (-3,2) \to (-3,1) \to (-3,0) \to (-3,-1) \to (-2,-1) \to (-1,-1) \to (0,-1) \to (0,0)\(\)
\(\)(0,0) \to (0,1) \to (0,2) \to (-1, 2) \to (-2,2) \to (-3,2) \to (-3,1) \to (-3,0) \to (-3,-1) \to (-2,-1) \to (-1,-1) \to (0,-1) \to (0,0)\(\) В третьем примере можно собрать все коробки не делая шагов.