Майкл и Джо играют в игру. Игра ведется в табличке с \(n\) строками и \(m\) столбцами, заполненной попарно различными целыми числами. Обозначим ячейку в \(i\)-й (\(1\le i\le n\)) строке и \(j\)-м (\(1\le j\le m\)) столбце через \((i, j)\), а число в ней через \(a_{ij}\).
Майкл начинает с того, что называет два числа \(h\) (\(1\le h \le n\)) и \(w\) (\(1\le w \le m\)). Затем Джо выбирает любой подпрямоугольник доски размером \(h\times w\) (так, чтобы Майкл не видел).
Формально, подпрямоугольник \(h\times w\) начинается с некоторой ячейки \((a,b)\), где \(1 \le a \le n-h+1\) и \(1 \le b \le m-w+1\). Он содержит все ячейки \((i,j)\) с \(a \le i \le a+h-1\) и \(b \le j \le b+w-1\).
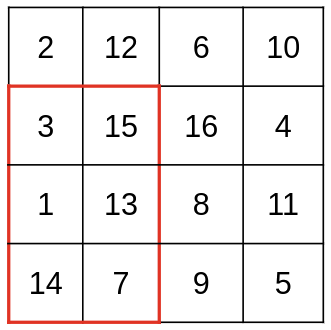Возможный ход Джо, если Майкл скажет \(3\times 2\) (с максимумом в \(15\)). Наконец, Майкл должен угадать максимальное число в выбранном подпрямоугольнике. Он выигрывает, если угадает правильно.
Так как Майкл не любит большие числа, он хочет, чтобы площадь выбранного подпрямоугольника (то есть \(h \cdot w\)) была как можно меньше, но чтобы при этом он мог выиграть, независимо от выбора Джо. Помогите Майклу найти эту минимально возможную площадь.
Можно показать, что Майкл всегда может выбрать \(h, w\), для которых он может гарантировать свой выигрыш.
Примечание
В первом примере таблица имеет размер \(1\times 1\), поэтому единственным возможным выбором для \(h, w\) является \(h = 1, w = 1\), что дает площадь \(h\cdot w = 1\).
Таблица из второго набора входных данных нарисована в условии. Можно показать, что при \(h = 3, w = 3\) Майкл может гарантировать победу и что любой выбор с \(h\cdot w \le 8\) победы не гарантирует.