Дан ориентированный ацикличный граф, состоящий из \(n\) вершин и \(m\) ребер. Вершины пронумерованы от \(1\) до \(n\). В графе нет кратных ребер и петель.
Пусть \(\mathit{in}_v\) будет количеством входящих ребер (степень входа), а \(\mathit{out}_v\) будет количеством исходящих ребер (степень исхода) вершины \(v\).
Требуется удалить некоторые ребра из графа. Пусть новые степени будут \(\mathit{in'}_v\) и \(\mathit{out'}_v\).
Разрешается удалять ребра, только если выполняются следующие условия для каждой вершины \(v\):
- \(\mathit{in'}_v < \mathit{in}_v\) or \(\mathit{in'}_v = \mathit{in}_v = 0\);
- \(\mathit{out'}_v < \mathit{out}_v\) or \(\mathit{out'}_v = \mathit{out}_v = 0\).
Назовем множество вершин \(S\) красивым, если для каждой пары вершин \(v\) и \(u\) (\(v \neq u\)), таких, что \(v \in S\) и \(u \in S\), существует путь либо из \(v\) в \(u\), либо из \(u\) в \(v\) по неудаленным ребрам.
Какой максимальный возможный размер красивого множества \(S\) после того, как вы удалите некоторые ребра из графа, а степени входа и исхода всех вершин либо уменьшатся, либо останутся равны \(0\)?
Выходные данные
Выведите одно целое число — максимальный возможный размер красивого множества \(S\) после того, как вы удалите некоторые ребра из графа, а степени входа и исхода всех вершин либо уменьшатся, либо останутся равны \(0\).
Примечание
В первом примере можно удалить ребра \((1, 2)\) и \((2, 3)\). \(\mathit{in} = [0, 1, 2]\), \(\mathit{out} = [2, 1, 0]\). \(\mathit{in'} = [0, 0, 1]\), \(\mathit{out'} = [1, 0, 0]\). Можно видеть, что для всех \(v\) условия выполняются. Максимальное красивое множество \(S\) образовано вершинами \(1\) и \(3\). Они все еще соединены ребром напрямую, поэтому между ними есть путь.
Во втором примере нет ребер. Так как все \(\mathit{in}_v\) и \(\mathit{out}_v\) равны \(0\), оставить граф с нулем ребер разрешено. Есть \(5\) красивых множеств, в каждом содержится одна вершина. Поэтому максимальный размер множества равен \(1\).
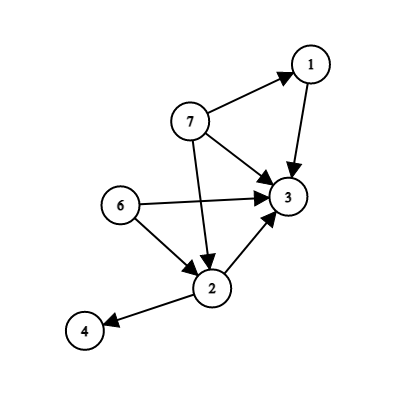
В третьем примере можно удалить ребра \((7, 1)\), \((2, 4)\), \((1, 3)\) и \((6, 2)\). Максимальное красивое множество \(S = \{7, 3, 2\}\). Можно еще удалить ребро \((7, 3)\), и ответ не изменится.
Изображение графа с третьего примера:
Примеры
| № | Входные данные | Выходные данные |
|
1
|
3 3
1 2
2 3
1 3
|
2
|
|
2
|
5 0
|
1
|
|
3
|
7 8
7 1
1 3
6 2
2 3
7 2
2 4
7 3
6 3
|
3
|