Вам задана двоичная матрица \(A\) размера \(n \times n\). Строки пронумерованы сверху вниз от \(1\) до \(n\), столбцы пронумерованы слева направо от \(1\) до \(n\). Ячейка, находящаяся на пересечении строки \(i\) и столбца \(j\) называется \(A_{ij}\). Рассмотрим набор из \(4\) операций:
- Циклически сдвинуть все строки вверх. Строка с номером \(i\) будет записана на место строки \(i-1\) (\(2 \le i \le n\)), строка с номером \(1\) будет записана на место строки \(n\).
- Циклически сдвинуть все строки вниз. Строка с номером \(i\) будет записана на место строки \(i+1\) (\(1 \le i \le n - 1\)), строка с номером \(n\) будет записана на место строки \(1\).
- Циклически сдвинуть все столбцы влево. Столбец с номером \(j\) будет записан на место столбца \(j-1\) (\(2 \le j \le n\)), столбец с номером \(1\) будет записан на место столбца \(n\).
- Циклически сдвинуть все столбцы вправо. Столбец с номером \(j\) будет записан на место столбца \(j+1\) (\(1 \le j \le n - 1\)), столбец с номером \(n\) будет записан на место столбца \(1\).
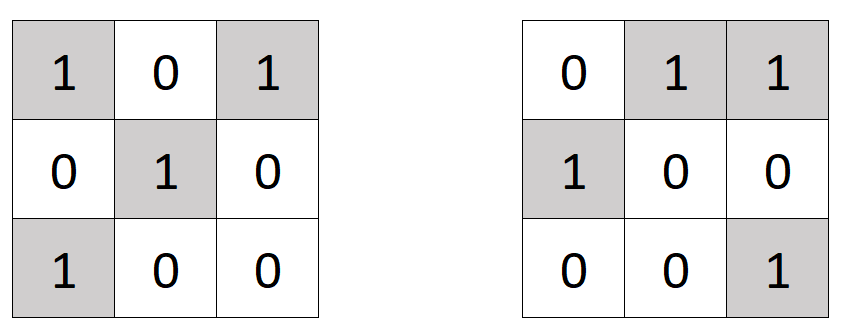Слева изображена матрица \(3 \times 3\) до применения к ней операции \(3\), справа — после. Вы можете провести над матрицей произвольное (возможно, нулевое) количество операций, операции можно проводить в любом порядке.
После этого вы можете осуществить произвольное (возможно, нулевое) количество новых xor-операций:
- Выбрать любую ячейку \(A_{ij}\) и записать в нее значение выражения \(A_{ij} \oplus 1\). Другими словами, в ячейку \(A_{ij}\) необходимо будет записать значение \((A_{ij} + 1) \bmod 2\).
Каждое применение этой xor-операции стоит один бурль. Заметим, что \(4\) операции сдвигов — бесплатные. Эти \(4\) операции можно проводить только до осуществления xor-операций.
Выведите минимальное количество бурлей, сколько придётся заплатить, чтобы сделать матрицу \(A\) единичной. Единичной называется такая матрица, на главной диагонали которой стоят единицы, а остальные её элементы являются нулями (то есть, \(A_{ij} = 1\) при \(i = j\) и \(A_{ij} = 0\) иначе).
Выходные данные
Для каждого набора входных данных выведите минимальное количество бурлей, сколько придётся заплатить, чтобы сделать матрицу \(A\) единичной. Иными словами, выведите минимальное количество xor-операций, которое потребуется совершить после применения циклических сдвигов к матрице, для того, чтобы матрица \(A\) стала единичной.
Примечание
В первом наборе входных данных можно действовать следующим образом: сначала циклически сдвинуть все строки вниз, тогда на главной диагонали матрицы будут стоять одни единицы. Затем необходимо будет применить xor-операцию к единственной единице, которая окажется не на главной диагонали.
Во втором наборе входных данных можно получить единичную матрицу, дважды применив к матрице операцию \(2\) — циклический сдвиг строк вверх.
Примеры
| № | Входные данные | Выходные данные |
|
1
|
4
3
010
011
100
5
00010
00001
10000
01000
00100
2
10
10
4
1111
1011
1111
1111
|
1
0
2
11
|