Вам задан тетраэдр. Обозначим его вершины буквами A, B, C и D соответственно.
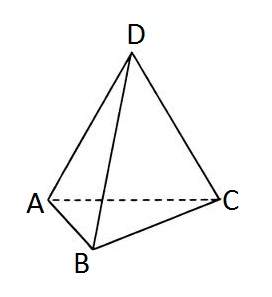
В вершине тетраэдра D находится муравей. Муравей очень подвижный и не любит стоять на месте. В каждый момент времени он совершает один шаг от одной вершины к другой по некоторому ребру тетраэдра, оставаться на месте он не может.
От Вас в этой задаче требуется совсем немногое: нужно посчитать каким количеством способов муравей может прийти из исходной вершины D в себя ровно за n шагов. Другими словами, Вас просят узнать количество различных циклических путей длины n из вершины D в себя. Поскольку это количество может быть достаточно большим, ответ требуется посчитать по модулю 1000000007 (109 + 7).
Выходные данные
Выведите единственное целое число — искомое количество способов по модулю 1000000007 (109 + 7).
Примечание
Искомые пути в первом примере:
- D - A - D
- D - B - D
- D - C - D
Примеры
| № | Входные данные | Выходные данные |
|
1
|
2
|
3
|
|
2
|
4
|
21
|