Рассмотрим турнир по системе плей-офф, в котором участвуют \(2^n\) спортсменов. Спортсмены пронумерованы от \(1\) до \(2^n\).
Турнир проходит в \(n\) этапов. На каждом этапе спортсмены делятся на пары таким образом, что каждый оказывается ровно в одной паре. В каждой паре атлеты соревнуются друг с другом, и один из них побеждает. Победитель проходит в следующий этап турнира, проигравший покидает турнир.
Пары формируются следующим образом:
- на первом этапе спортсмен \(1\) соревнуется со спортсменом \(2\); \(3\) соревнуется с \(4\); \(5\) соревнуется с \(6\), и так далее;
- на втором этапе победитель пары «\(1\)–\(2\)» соревнуется с победителем пары «\(3\)–\(4\)»; победитель пары «\(5\)–\(6\)» соревнуется с победителем пары «\(7\)–\(8\)», и так далее;
- следующие этапы проходят по той же закономерности.
Когда соревнуются спортсмены \(x\) и \(y\), победитель выбирается следующим образом:
- если \(x+y\) нечетно, побеждает спортсмен с меньшим номером (то есть, если \(x < y\), то побеждает \(x\), иначе побеждает \(y\));
- если \(x+y\) четно, побеждает спортсмен с большим номером.
На картинке показано, как проходит турнир при \(n = 3\).
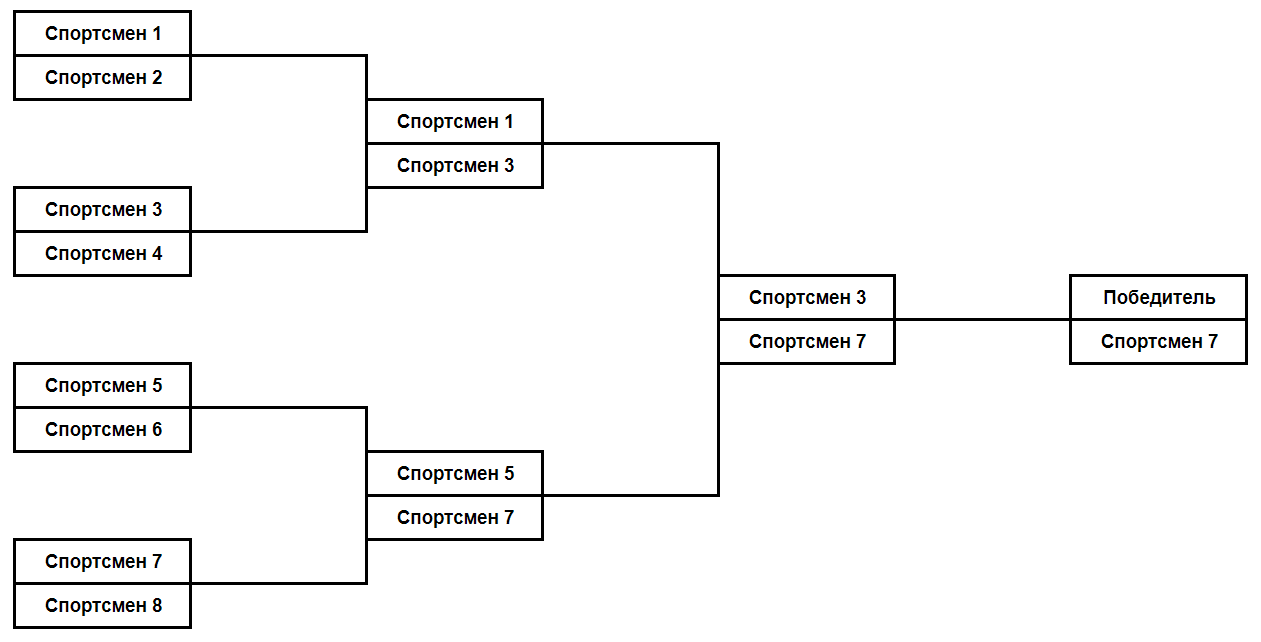
Ваша задача состоит в следующем: по заданному числу \(n\) определите номер спортсмена, который будет победителем турнира.
Примечание
Случай \(n = 3\) разобран на картинке в условии.
Если \(n = 1\), то в турнире соревнуются только спортсмены \(1\) и \(2\). Так как \(1 + 2 = 3\) — нечетное число, спортсмен с меньшим номером побеждает. Поэтому спортсмен \(1\) — победитель турнира.