Два маляра, Амин и Бенджи, перекрашивают потолок в гостиной Грегора! Потолок можно представить как таблицу размера \(n \times m\).
Для каждого \(i\) от \(1\) до \(n\) включительно маляр Амин нанес \(a_i\) слоев краски на весь \(i\)-й ряд. Для каждого \(j\) от \(1\) до \(m\) включительно маляр Бенджи нанес \(b_j\) слоев краски на весь \(j\)-й столбец. Таким образом, клетка \((i,j)\) оказалась покрашенной в \(a_i+b_j\) слоев краски.
Грегор считает, что клетка \((i,j)\) плохо покрашена, если \(a_i+b_j \le x\). Определим плохо покрашенную область как максимальную по включению связную компоненту плохо покрашенных клеток, то есть такую связную компоненту плохо покрашенных клеток, что все клетки, соседние с этой компонентой, не являются плохо покрашенными. Две клетки являются соседними, если они имеют общую сторону.
Грегор потрясен состоянием потолка, покрашенного малярами, и хочет знать количество плохо покрашенных областей.
Выходные данные
Выведите одно целое число — количество плохо покрашенных областей.
Примечание
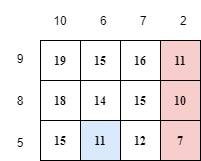
Рисунок ниже иллюстрирует первый пример. Числа слева от каждого ряда представляют собой список \(a\), а числа над каждым столбцом — список \(b\). Числа внутри каждой клетки равны количеству слоев краски в этой клетке.
Цветные клетки соответствуют плохо покрашенным клеткам. Красные и синие клетки соответственно образуют \(2\) плохо покрашенных области.
Примеры
| № | Входные данные | Выходные данные |
|
1
|
3 4 11
9 8 5
10 6 7 2
|
2
|
|
2
|
3 4 12
9 8 5
10 6 7 2
|
1
|
|
3
|
3 3 2
1 2 1
1 2 1
|
4
|
|
4
|
5 23 6
1 4 3 5 2
2 3 1 6 1 5 5 6 1 3 2 6 2 3 1 6 1 4 1 6 1 5 5
|
6
|