У подножия горы Лиюшань будут установлены \(n\) палаток, для тех, кто желает испытать радость от единения с природой, спокойствия ночи и яркого звездного неба.
Палатка номер \(i\) будет расположена в точке \((x_i, y_i)\) и будет иметь вес \(w_i\). Палатка считается важной, если оба \(x_i\) и \(y_i\) являются четными. Вам нужно убрать некоторые из палаток так, чтобы для каждой оставшейся важной палатки \((x, y)\) не существовало \(3\) другие палатки \((x'_1, y'_1)\), \((x'_2, y'_2)\) и \((x'_3, y'_3)\), такие что оба условия выполнены:
- \(|x'_j-x|, |y'_j - y|\leq 1\) для всех \(j \in \{1, 2, 3\}\).
- Эти четыре палатки образуют параллелограмм (или прямоугольник), и одна из его сторон параллельна оси \(x\).
Максимизируйте сумму весов оставшихся палаток.
Выходные данные
Выведите одно целое число — максимальную сумму весов оставшихся палаток.
Примечание
Иллюстрация для второго примера. Черные треугольники обозначают важные палатки. Этот пример также показывает все \(8\) запрещенных паттернов.
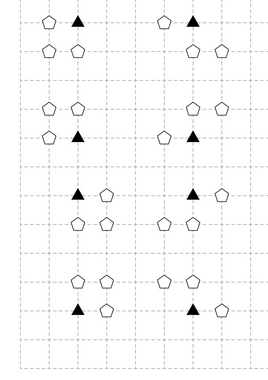
Примеры
| № | Входные данные | Выходные данные |
|
1
|
5
0 0 4
0 1 5
1 0 3
1 1 1
-1 1 2
|
12
|
|
2
|
32
2 2 1
2 3 1
3 2 1
3 3 1
2 6 1
2 5 1
3 6 1
3 5 1
2 8 1
2 9 1
1 8 1
1 9 1
2 12 1
2 11 1
1 12 1
1 11 1
6 2 1
7 2 1
6 3 1
5 3 1
6 6 1
7 6 1
5 5 1
6 5 1
6 8 1
5 8 1
6 9 1
7 9 1
6 12 1
5 12 1
6 11 1
7 11 1
|
24
|