Вам дан массив \(a\) из \(n\) (\(n \geq 2\)) положительных целых чисел, а также целое число \(p\). Рассмотрим неориентированный взвешенный граф на \(n\) вершинах, пронумерованных от \(1\) до \(n\), в котором между вершинами \(i\) и \(j\) (\(i<j\)) добавлены следующие ребра:
- Если \(gcd(a_i, a_{i+1}, a_{i+2}, \dots, a_{j}) = min(a_i, a_{i+1}, a_{i+2}, \dots, a_j)\), то между вершинами \(i\) и \(j\) существует ребро веса \(min(a_i, a_{i+1}, a_{i+2}, \dots, a_j)\).
- Если \(i+1=j\), то между вершинами \(i\) и \(j\) существует ребро веса \(p\).
Здесь \(gcd(x, y, \ldots)\) обозначает наибольший общий делитель (НОД) чисел \(x\), \(y\), ....
Обратите внимание, между вершинами \(i\) и \(j\) появляются кратные ребра, если оба условия выполнены. Если же ни одно условие не выполнено для \(i\) и \(j\), то между ними нет ребер.
Ваша цель — найти вес минимального остовного дерева данного графа.
Выходные данные
Выведите \(t\) строк. Для каждого набора входных данных выведите вес соответствующего минимального остовного дерева.
Примечание
Ниже изображены графы для четырех наборов входных данных примера (ребра одного из минимальных остовных деревьев показаны розовым):
Набор 1
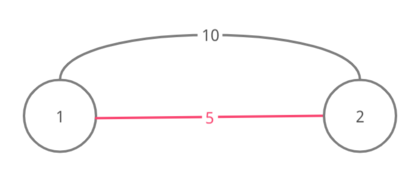
Набор 2
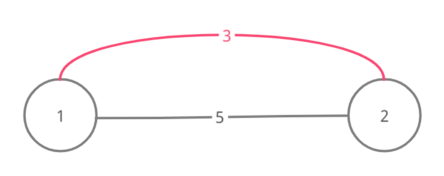
Набор 3
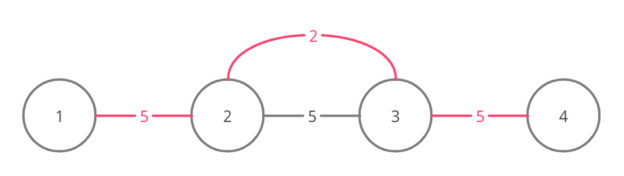
Набор 4
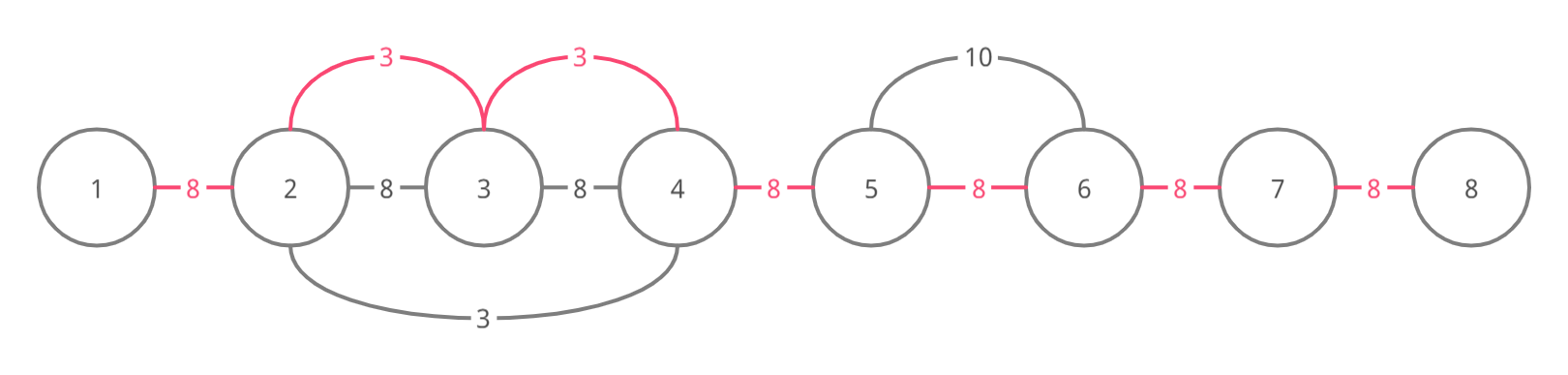
Примеры
| № | Входные данные | Выходные данные |
|
1
|
4
2 5
10 10
2 5
3 3
4 5
5 2 4 9
8 8
5 3 3 6 10 100 9 15
|
5
3
12
46
|