В Сингапурском зоопарке появилась новая достопримечательность: Бесконечный Зоопарк.
Бесконечный Зоопарк может быть представлен графом с бесконечным числом вершин, обозначенных \(1,2,3,\ldots\). От вершины \(u\) до вершины \(u+v\) существует ориентированное ребро, если и только если \(u\&v=v\), где \(\&\) обозначает операцию побитового И. Других ребер в графе нет.
Хранительница Зоопарка получила \(q\) запросов. В \(i\)-м запросе она спросит вас, может ли она добраться от вершины \(u_i\) до вершины \(v_i\) по ориентированным ребрам.
Выходные данные
Для \(i\)-го из \(q\) запросов выведите «YES» в единственной строке, если Хранительница Зоопарка может добраться от вершины \(u_i\) до вершины \(v_i\). В противном случае выведите «NO».
Ответ можно вывести в любом регистре. Например, если ответ «YES», то вывод «Yes» или «yeS» также будет считаться правильным ответом.
Примечание
Ниже показан подграф на вершинах \(1,2,3,4,5,6\).
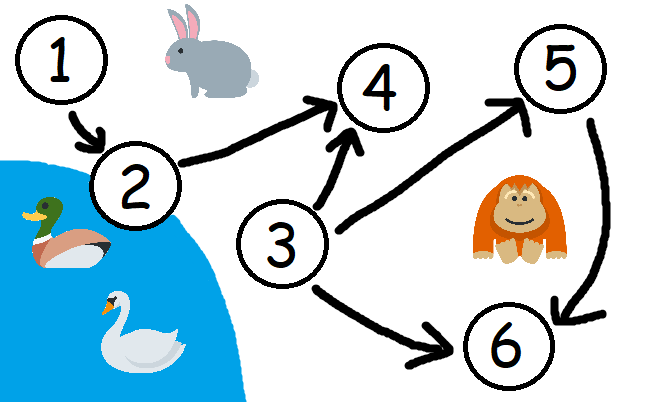
Примеры
| № | Входные данные | Выходные данные |
|
1
|
5
1 4
3 6
1 6
6 2
5 5
|
YES
YES
NO
NO
YES
|