Вы и ваши друзья живете в \(n\) домах. Каждый дом расположен на 2D плоскости в точке с целыми координатами. Несколько домов могут быть расположены в одной точке. Мэр города хочет узнать у вас возможные места для постройки здания Восточной выставки. Найдите количество мест (точек с целыми координатами) таких, что суммарное расстояние от всех домов до выставки будет минимальным. Здание выставки может быть построено в той же точке, что и какой-то дом. Расстояние между двумя точками \((x_1, y_1)\) и \((x_2, y_2)\) считается по формуле \(|x_1 - x_2| + |y_1 - y_2|\), где \(|x|\) — модуль величины \(x\).
Выходные данные
Для каждого набора входных данных выведите единственное число — количество различных позиций для здания выставки. Здание выставки может быть построено в той же точке, что и какой-то дом.
Примечание
Снизу находятся картинки поясняющие примеры. Голубые точки обозначают дома, а зеленые - возможные позиции для выставки.
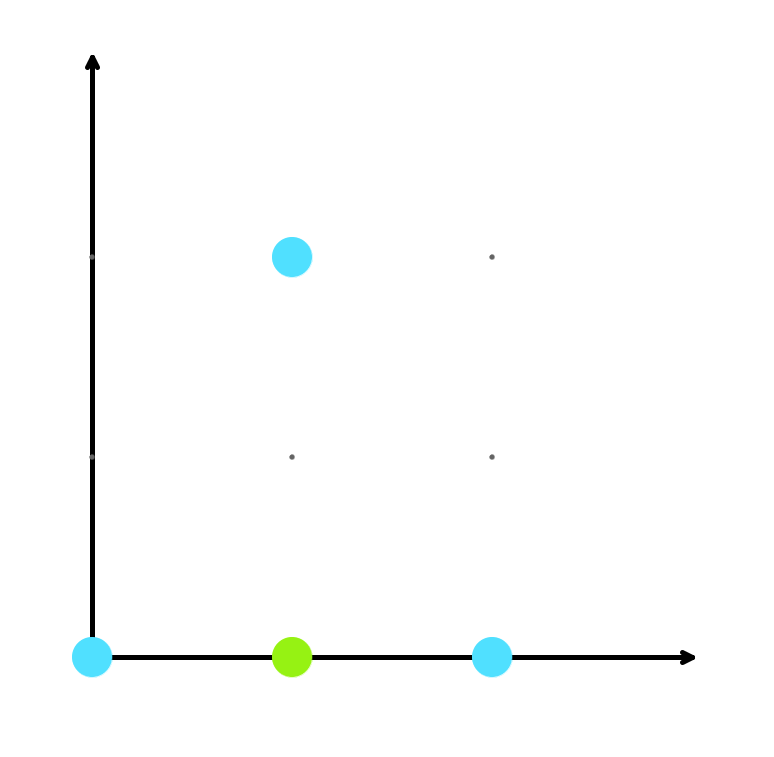
Первый пример.
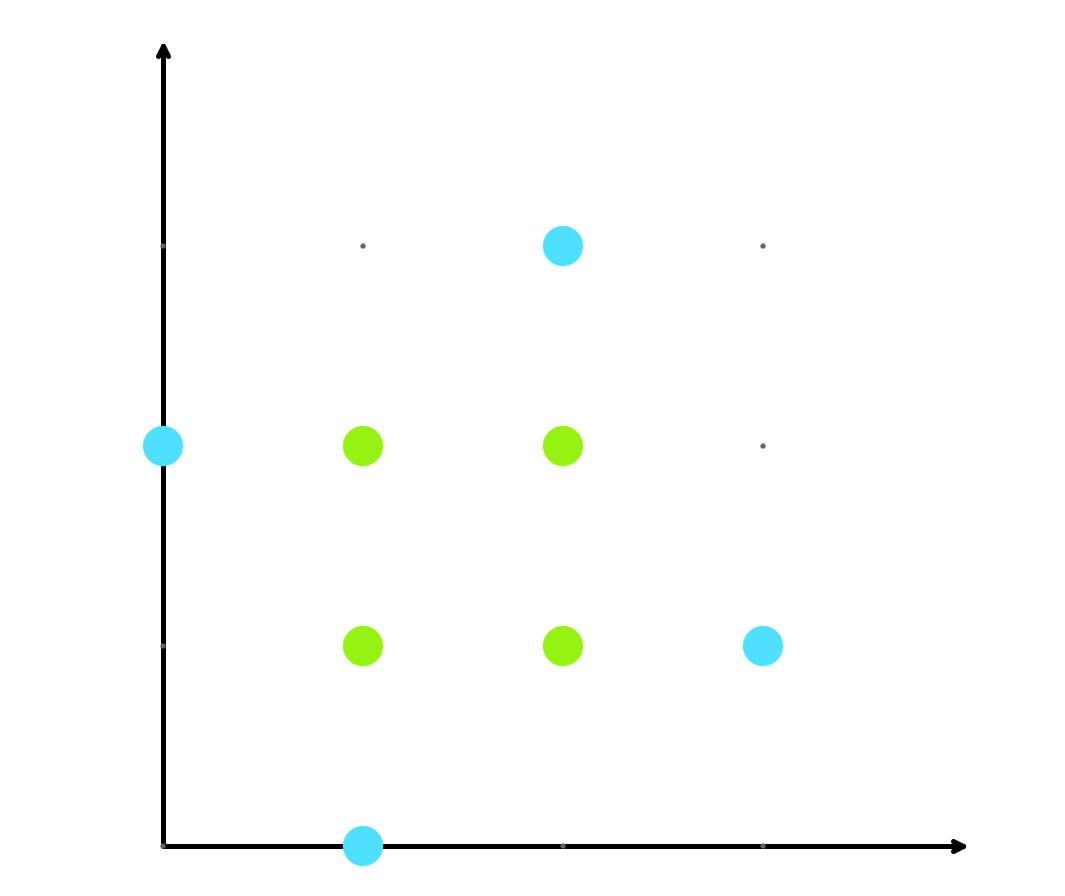
Второй пример.
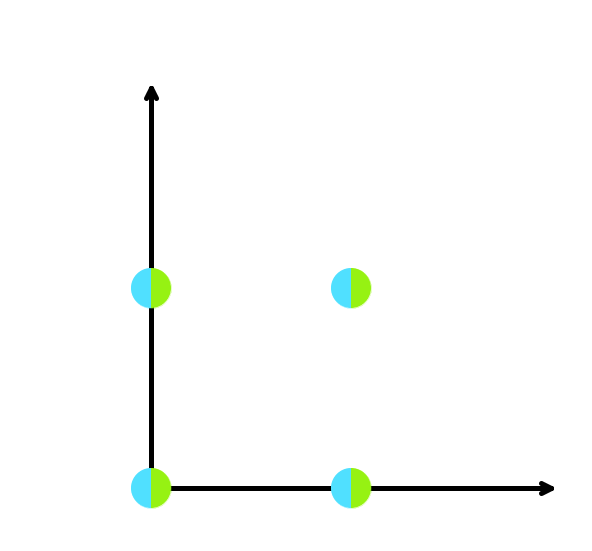
Третий пример. 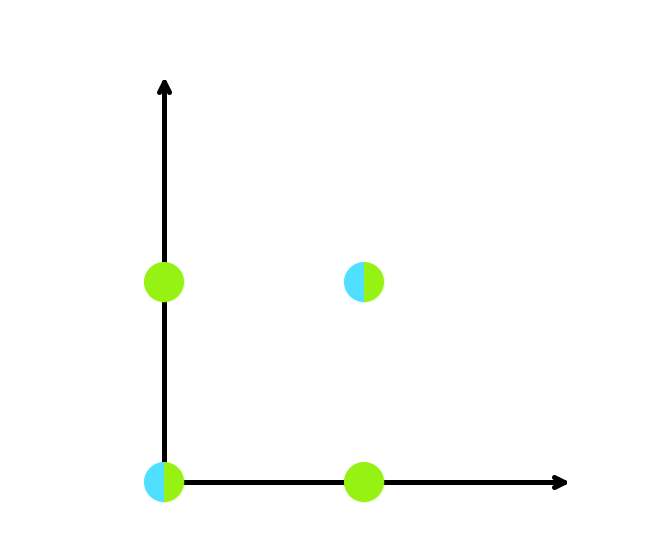
Четвертый пример. 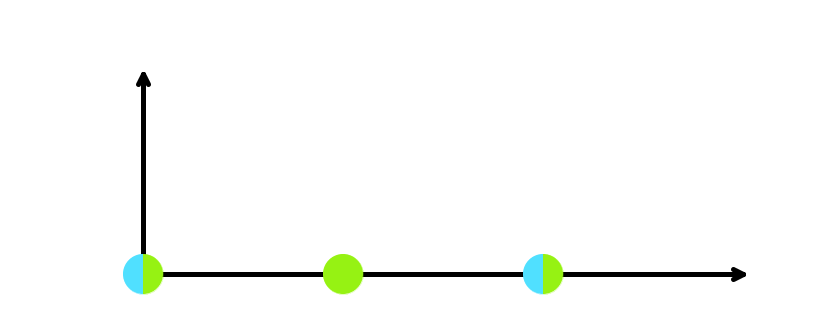
Пятый пример. 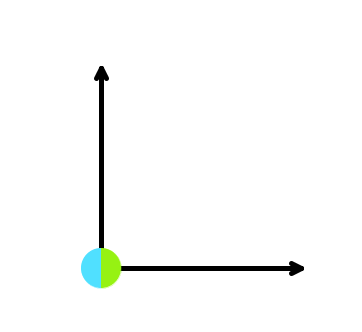
Шестой пример. Оба дома находятся в позиции \((0, 0)\).
Примеры
| № | Входные данные | Выходные данные |
|
1
|
6
3
0 0
2 0
1 2
4
1 0
0 2
2 3
3 1
4
0 0
0 1
1 0
1 1
2
0 0
1 1
2
0 0
2 0
2
0 0
0 0
|
1
4
4
4
3
1
|