Олимпиадный тренинг

Задача . E. Две платформы

Задача

Темы: Бинарный поиск два указателя дп сортировки *1800

На плоскости находится $n$ точек. Точка $i$ имеет координаты $(x_i, y_i)$. У вас есть две горизонтальные платформы, обе длины $k$. Каждая платформа может быть размещена в любом месте на плоскости, но она должна быть размещена горизонтально (на одной и той же $y$-координате) и иметь целочисленные границы. Если левая граница платформы равна $(x, y)$, то правая граница равна $(x + k, y)$, и все точки между границами (включая границы) принадлежат платформе.

Обратите внимание, что платформы могут иметь общие точки (пересекаться), а также не обязательно размещать обе платформы на одной $y$-координате.

После размещения обеих платформ на плоскости все точки начинают падать вниз, уменьшая $y$-координату. Если в какой-то момент точка сталкивается с какой-либо платформой, то она останавливается и считается сохраненной. Точки, которые никогда не сталкиваются ни с какой платформой, теряются.

Ваша задача — найти максимальное количество точек, которые вы можете сохранить, если вы разместите обе платформы оптимально.

Вам необходимо ответить на $t$ независимых наборов тестовых данных.

Для лучшего понимания, пожалуйста, ознакомьтесь с разделом Примечание ниже, чтобы увидеть картинку для первого набора тестовых данных примера.

Входные данные

Первая строка входных данных содержит одно целое число $t$ ($1 \le t \le 2 \cdot 10^4$) — количество наборов тестовых данных. Затем следует $t$ наборов тестовых данных.

Первая строка набора тестовых данных содержит два целых числа $n$ и $k$ ($1 \le n \le 2 \cdot 10^5$; $1 \le k \le 10^9$) — количество точек и длину каждой платформы, соответственно. Вторая строка набора тестовых данных содержит $n$ целых чисел $x_1, x_2, \dots, x_n$ ($1 \le x_i \le 10^9$), где $x_i$ — это $x$-координата $i$-й точки. Третья строка набора тестовых данных содержит $n$ целых чисел $y_1, y_2, \dots, y_n$ ($1 \le y_i \le 10^9$), где $y_i$ — это $y$-координата $i$-й точки. Все точки различны (не существует такой пары $1 \le i < j \le n$, что $x_i = x_j$ и $y_i = y_j$).

Гарантируется, что сумма $n$ не превосходит $2 \cdot 10^5$ ($\sum n \le 2 \cdot 10^5$).

Выходные данные

Выведите ответ на каждый набор тестовых данных: максимальное количество точек, которые вы можете сохранить, если вы разместите обе платформы оптимально.

Примечание

Картинка, соответствующая первому набору тестовых данных примера:

$\text{[math]}$

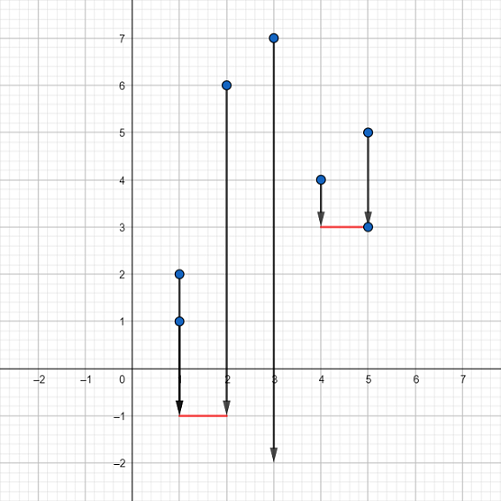
Синие точки представляют собой точки из входных данных, красные отрезки — платформы. Одним из возможных способов является размещение первой платформы между точками $(1, -1)$ и $(2, -1)$, а второй платформы — между точками $(4, 3)$ и $(5, 3)$. Векторы обозначают, как будут падать точки. Можно заметить, что единственная точка, которую мы не можем сохранить — это точка $(3, 7)$, поэтому она будет падать бесконечно и в итоге будет потеряна. Можно доказать, что мы не можем добиться лучшего ответа. Также обратите внимание, что точка $(5, 3)$ вообще не падает, потому что она уже находится на платформе.

Примеры

№	Входные данные	Выходные данные
1	4 7 1 1 5 2 3 1 5 4 1 3 6 7 2 5 4 1 1 1000000000 1000000000 5 10 10 7 5 15 8 20 199 192 219 1904 10 10 15 19 8 17 20 10 9 2 10 19 12 13 6 17 1 14 7 9 19 3	6 1 5 10

time 2000 ms
memory 256 Mb
Правила оформления программ и список ошибок при автоматической проверке задач

Статистика успешных решений по компиляторам

	Кол-во
С++ Mingw-w64	5

Комментарий учителя

Ваш ответ

выберите язык и введите исходный код

Для отправки решения задачи необходимо зарегистрироваться или авторизоваться!

Загруженные файлы

Нет