Ильдар учитель алгоритмов у Вильяма и Харриса. Сегодня, Ильдар рассказывает Декартово дерево. К сожалению, Харрис заболел, поэтому Ильдар учит сегодня только Вильяма.
Декартово дерево это корневое дерево, которое может быть построено с помощью последовательности различных целых чисел. Мы строим декартово дерево следующим образом:
- Если последовательность пустая, верните пустое дерево;
- Пусть позиция максимального элемента это \(x\);
- Удалите элемент на позиции \(x\) из последовательности и разбейте ее на левую и правую часть от этого элемента (которые могут оказаться пустыми) (элемент на самом деле нужно не удалить навсегда, а временно забрать из последовательности);
- Постройте декартово дерево для каждой части;
- Сделайте новую вершину для элемента, который был на позиции \(x\), который станет корнем всего дерева. Теперь, если корни декартовых деревьев для левой и правой части существовали, они становятся сыновьями для этой вершины;
- Верните полученное дерево.
Например, это декартово дерево для последовательности \(4, 2, 7, 3, 5, 6, 1\):
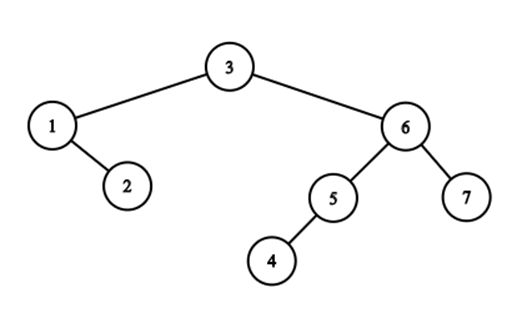
После того, как Ильдар рассказал про декартово дерево, он задал домашнее задание. Он начинает с пустой последовательности \(a\).
В \(i\)-м раунде, он добавляет число \(i\) куда-то в \(a\). Затем, он задает вопрос: чему равна сумма размеров поддеревьев для всех вершин в декартовом дереве текущей последовательности \(a\)?
Вершина \(v\) находится в поддереве вершины \(u\), тогда и только тогда, когда \(v = u\) или \(v\) находится в одном из поддеревьев одного из сыновей вершины \(u\). Размер поддерева вершины \(u\) равен количеству вершин \(v\), таких что \(v\) находится в поддереве вершины \(u\).
Всего Ильдар проведет \(n\) раундов. В качестве домашней работы он просит дать ответ на эти \(n\) вопросов.
На следующий день, Ильдар сказал Харрису, что он тоже должен выполнить это домашнее задание. Харрис получил финальное состояние последовательности \(a\) от Вильяма. К сожалению, у него нету идей как получить ответы на эти \(n\) вопросов. Помогите Харрису!
Примечание
После первого раунда, последовательность это \(1\). Дерево выглядит так:

Ответ равен \(1\).
После второго раунда, последовательность это \(2, 1\). Дерево выглядит так:
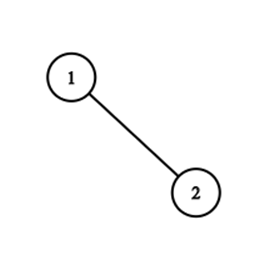
Ответ равен \(2+1=3\).
После третьего раунда, последовательность это \(2, 1, 3\). Дерево выглядит так:
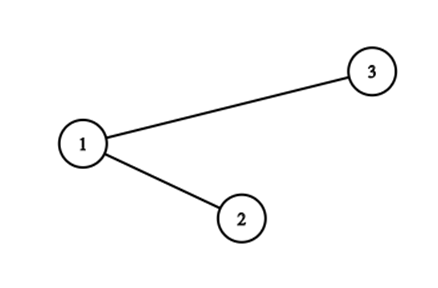
Ответ равен \(2+1+3=6\).
После четвертого раунда, последовательность это \(2, 4, 1, 3\). Дерево выглядит так:
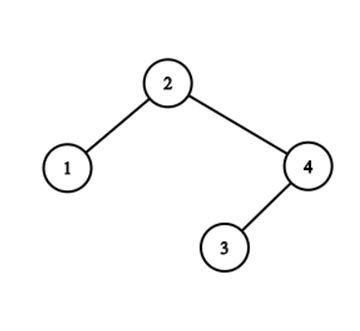
Ответ равен \(1+4+1+2=8\).
После пятого раунда, последовательность это \(2, 4, 1, 5, 3\). Дерево выглядит так:
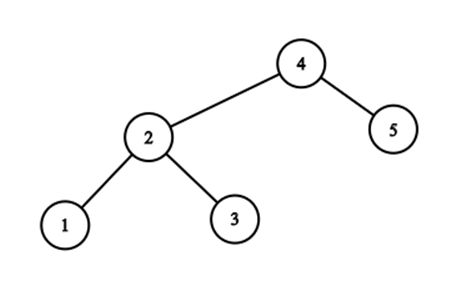
Ответ равен \(1+3+1+5+1=11\).