В Чилляндии построили бесконечно длинный Линейный Чилляндский Коллайдер (ЛЧК). К ЛЧК подсоединены \(n\) труб c координатами \(x_i\). В момент времени 0 из каждой трубки ЛЧК вылетает протон направо с вероятностью \(p_i\) и с вероятностью \((1 - p_i)\) — влево. Протон \(i\) разогнан до скорости \(v_i\). Длительность эксперимента определяется как время до первого столкновения двух протонов. В случае, если столкновений не произойдет, длительность эксперимента полагается равной нулю.
Найдите математическое ожидание длительности эксперимента.
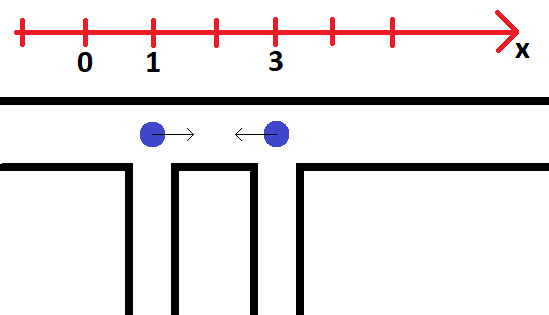Иллюстрация к первому примеруВыходные данные
Можно показать, что ответ всегда можно представить в виде дроби \(P/Q\), где \(P\) — целое число, а \(Q\) — натуральное число, не кратное \(998\,244\,353\). В таком случае выведите \(P \cdot Q^{-1}\) по модулю \(998\,244\,353\).
Примеры
| № | Входные данные | Выходные данные |
|
1
|
2
1 1 100
3 1 0
|
1
|
|
2
|
3
7 10 0
9 4 86
14 5 100
|
0
|
|
3
|
4
6 4 50
11 25 50
13 16 50
15 8 50
|
150902884
|