Боб играет со стандартными \(6\)-гранными костями (кубиками). Развертка стандартного кубика приведена на рисунке ниже.
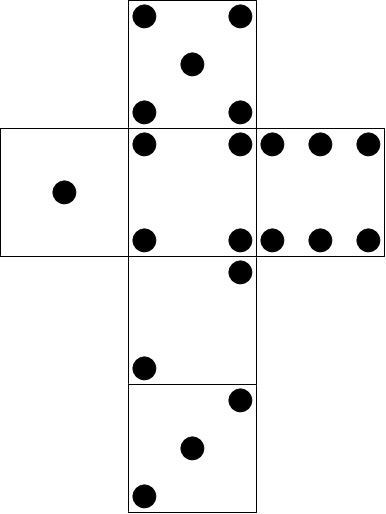
У Боба есть бесконечное число игральных кубиков, и он хочет построить из них башню, ставя один кубик на другой и выбирая ориентацию каждого нового кубика. После того, как Боб построит башню, он посчитает количество видимых точек на гранях кубиков.
Например, количество видимых точек на башне, нарисованной ниже, равно \(29\) — число точек на верхней грани верхнего кубика равно \(1\), а с четырех сторон башни видны грани со следующим количеством точек: \(5\) и \(3\) с южной стороны, \(4\) и \(2\) с западной стороны, \(2\) и \(4\) с северной стороны, и \(3\) и \(5\) с восточной стороны.
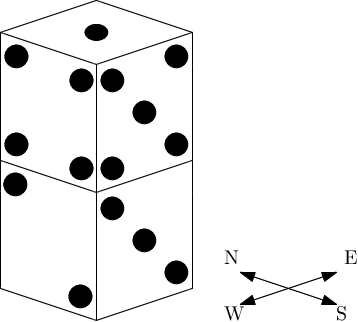
Нижняя грань первого кубика (с единицей) и грани с шестью точками не видны, поэтому они не учитываются в количестве видимых точек.
У Боба есть \(t\) любимых чисел \(x_i\). Для каждого из чисел \(x_i\) помогите Бобу узнать, можно ли построить башню из кубиков, для которой количество видимых точек равно этому числу.
Выходные данные
Для каждого любимого числа Боба выведите «YES», если можно построить башню, или «NO» в противном случае (без кавычек).
Примечание
Первый пример разобран в условии.
Ответ на второй пример можно получить, если перевернуть верхний кубик на башне из условия.
В третьем примере достаточно единственного кубика, поставленного таким образом, что на верхней грани изображено \(5\) точек.
В четвертом примере не существует башни с нужным количеством видимых точек.