Числа Фибоначчи имеют следующий вид:
F1 = 1, F2 = 2, Fi = Fi - 1 + Fi - 2, i > 2.Рассмотрим какое-либо непустое множество S = {s1, s2, ..., sk}, состоящее из различных чисел Фибоначчи, и найдем сумму значений элементов этого множества:
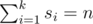
Будем называть множество S разложением в фибоначчиеву сумму числа n.
Нетрудно видеть, что некоторые числа имеют несколько разложений в фибоначчиеву сумму. Например, для 13 имеем 13, 5 + 8, 2 + 3 + 8 — три разложения, а для 16: 3 + 13, 1 + 2 + 13, 3 + 5 + 8, 1 + 2 + 5 + 8 — четыре разложения.
По заданному числу n определите количество его различных разложений в фибоначчиеву сумму.
Примечание
Два разложения различны если существует число, которое содержится в одном разложении, и не содержится в другом. Разложения, отличающиеся только порядком слагаемых, считаются одинаковыми.